K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
IA
19 tháng 2 2020
b,\(A=\frac{4}{3x-6}-\frac{x}{x^2-4}\)
\(A=\frac{4}{3\left(x-2\right)}-\frac{x}{\left(x-2\right)\left(x+2\right)}\)
\(A=\frac{4x+8}{3\left(x-2\right)\left(x+2\right)}-\frac{3x}{3\left(x-2\right)\left(x+2\right)}\)
\(A=\frac{x-8}{3\left(x-2\right)\left(x+2\right)}\)
c, Thay x = 1 vào A ta đc
\(\frac{1-8}{3\left(1-2\right)\left(1+2\right)}=\frac{7}{9}\)
19 tháng 2 2020
a) A xác định \(\Leftrightarrow\hept{\begin{cases}3x-6\ne0\\x^2-4\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}3x\ne6\\x^2\ne4\end{cases}\Leftrightarrow}\hept{\begin{cases}x\ne2\\x\ne\pm2\end{cases}\Leftrightarrow}x\ne\pm2}\)
Vậy A xác định khi \(x\ne\pm2\)
b) \(A=\frac{4}{3x-6}-\frac{x}{x^2-4}\left(x\ne\pm2\right)\)
\(\Leftrightarrow A=\frac{4}{3\left(x-2\right)}-\frac{x}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow A=\frac{4\left(x+2\right)}{3\left(x-2\right)\left(x+2\right)}-\frac{3x}{3\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow A=\frac{4x+8}{3\left(x+2\right)\left(x-2\right)}-\frac{3x}{3\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow A=\frac{4x+8-3x}{3\left(x-2\right)\left(x+2\right)}=\frac{x+8}{3\left(x-2\right)\left(x+2\right)}\)
Vậy \(A=\frac{x+8}{3\left(x-2\right)\left(x+2\right)}\left(x\ne\pm2\right)\)
c) Thay x=1 (tmđk) vào A ta có: \(A=\frac{1+8}{3\left(1-2\right)\left(1+2\right)}=\frac{9}{-9}=-1\)
Vậy \(A=-1\)khi x=1
3 tháng 10 2021
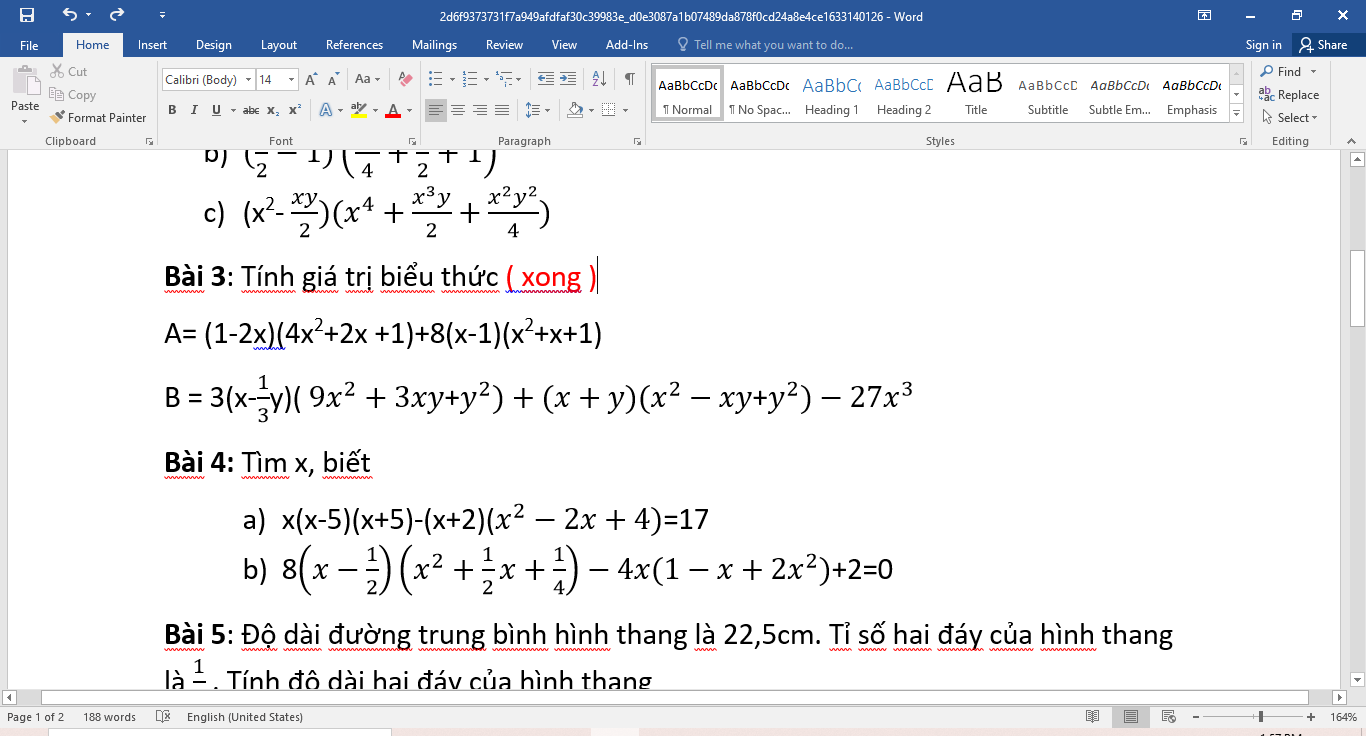
\(3,\\ A=1-8x^3+8x^3-8=-7\\ B=\left(3x-y\right)\left(9x^2+3xy+y^2\right)+x^3+y^3-27x^3\\ B=27x^3-y^3+x^3+y^3-27x^3=x^3\)
3 tháng 10 2021
Bài 4:
a: Ta có: \(x\left(x-5\right)\left(x+5\right)-\left(x+2\right)\left(x^2-2x+4\right)=17\)
\(\Leftrightarrow x^3-25x-x^3-8=17\)
\(\Leftrightarrow-25x=25\)
hay x=-1
b: Ta có: \(8\left(x-\dfrac{1}{2}\right)\left(x^2+\dfrac{1}{2}x+\dfrac{1}{4}\right)-4x\left(2x^2-x+1\right)+2=0\)
\(\Leftrightarrow8x^3-1-8x^3+4x^2-4x+2=0\)
\(\Leftrightarrow2x-1=0\)
hay \(x=\dfrac{1}{2}\)
TM
16 tháng 7 2019
bài 1:
2(x^2-9).4(x^2-1)
=(2x^2-18)(4x^2-4)
=8x^4-8x^2-72x^2+72
=8x^4-80x^2+72
16 tháng 7 2019
\(Bai1:2\left(x-3\right)\left(x+3\right)+4\left(x-1\right)\left(x+1\right)\)
\(=2\left(x^2-9\right)+4\left(x^2-1\right)\)
\(=2x^2-18+4x^2-4\)
\(=6x^2-22\)
\(Bai2:-\left(6x-1\right)\left(3-2x\right)+\left(3x-2\right)\left(4x-3\right)=17\)
\(\Leftrightarrow-\left(18x-12x^2-3+2x\right)+12x^2-9x-8x+6=17\)
\(\Leftrightarrow-18x+12x^2+3-2x+12x^2-9x-8x+6=17\)
\(\Leftrightarrow24x^2-37x+9-17=0\)
\(\Leftrightarrow24x^2-37x-8=0\)
Đề sai??
TG
21
1 tháng 10 2017
\(2x^2+2y^2-4xy+2x-2y+4\)
\(=2\left(x-y\right)^2+2\left(x-y\right)+4\)
\(=2\left[\left(x-y\right)^2+2\left(x-y\right)\frac{1}{2}+\frac{1}{4}\right]+\frac{7}{2}\)
\(=2\left(x-y+\frac{1}{2}\right)^2+\frac{7}{2}\)
\(\Rightarrow A\ge\frac{7}{2}\)
Dấu = bn tự tính nhé
NV
4
24 tháng 12 2021
7 + 4 = 11 chứ nhiu. cái câu này đến lớp 1 cũng biết hỏi. hỏi linh tinh
KN
4 tháng 8 2015
Quy trình ấn phím
X = X + 1 : A = 10A + 3 : B = B + A
Ấn CALC X? -1 =
A? 0 =
B? 0 =
Ấn = ... đến khi X = 12 thì ấn = = để nhận kq.
Kq = 3703703703699
15 tháng 10 2018
a) \(x^3+x^2y-x^2z-xyz\)
\(=x^2\left(x+y\right)-xz\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-xz\right)\)
\(=x\left(x+y\right)\left(x-z\right)\)
b) \(x^2-6x+9-9y^2\)
\(=\left(x^2-2\cdot x\cdot3+3^2\right)-\left(3y\right)^2\)
\(=\left(x-3\right)^2-\left(3y\right)^2\)
\(=\left(x-3-3y\right)\left(x-3+3y\right)\)
c) \(x^2+9x+20\)
\(=x^2+5x+4x+20\)
\(=x\left(x+5\right)+4\left(x+5\right)\)
\(=\left(x+5\right)\left(x+4\right)\)
d) \(x^4+4\)
\(=\left(x^2\right)^2+2\cdot x^2\cdot2+4-2\cdot x^2\cdot2\)
\(=\left(x^2+2\right)-\left(2x\right)^2\)
\(=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)
A
15 tháng 10 2018
a/\(x^3+x^2y-x^2z-xyz\)
\(=\left(x^3-x^2y\right)+\left(x^2y-xyz\right)\)
\(=x^2\left(x-z\right)+xy\left(x-z\right)\)
\(=\left(x-z\right)\left(x^2+xy\right)\)
b/\(x^2-6x+9-9y^2\)
\(=\left(x^2-6x+9\right)-9y^2\)
\(=\left(x-3\right)^2-\left(3y\right)^2\)
\(=\left(x-3+3y\right)\left(x-3-3y\right)\)
c/\(x^2+9x+20\)
\(=x^2+4x+5x+20\)
\(=\left(x^2+4x\right)+\left(5x+20\right)\)
\(=x\left(x+4\right)+5\left(x+4\right)\)
\(=\left(x+5\right)\left(x+4\right)\)
d/\(x^4+4\)
\(=x^4+4x^2-4x^2+4\)
\(=\left(x^2+4x^2+4\right)-4x^2\)
\(=\left(x+2\right)^2-\left(2x\right)^2\)
\(=\left(x+2-2x\right)\left(x+2+2x\right)\)