
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

Bài 1:
a.
$a^3-a^2c+a^2b-abc=a^2(a-c)+ab(a-c)$
$=(a-c)(a^2+ab)=(a-c)a(a+b)=a(a-c)(a+b)$
b.
$(x^2+1)^2-4x^2=(x^2+1)^2-(2x)^2=(x^2+1-2x)(x^2+1+2x)$
$=(x-1)^2(x+1)^2$
c.
$x^2-10x-9y^2+25=(x^2-10x+25)-9y^2$
$=(x-5)^2-(3y)^2=(x-5-3y)(x-5+3y)$
d.
$4x^2-36x+56=4(x^2-9x+14)=4(x^2-2x-7x+14)$
$=4[x(x-2)-7(x-2)]=4(x-2)(x-7)$
Bài 2:
a. $(3x+4)^2-(3x-1)(3x+1)=49$
$\Leftrightarrow (3x+4)^2-[(3x)^2-1]=49$
$\Leftrightarrow (3x+4)^2-(3x)^2=48$
$\Leftrightarrow (3x+4-3x)(3x+4+3x)=48$
$\Leftrightarrow 4(6x+4)=48$
$\Leftrightarrow 6x+4=12$
$\Leftrightarrow 6x=8$
$\Leftrightarrow x=\frac{4}{3}$
b. $x^2-4x+4=9(x-2)$
$\Leftrightarrow (x-2)^2=9(x-2)$
$\Leftrightarrow (x-2)(x-2-9)=0$
$\Leftrightarrow (x-2)(x-11)=0$
$\Leftrightarrow x-2=0$ hoặc $x-11=0$
$\Leftrightarrow x=2$ hoặc $x=11$
c.
$x^2-25=3x-15$
$\Leftrightarrow (x-5)(x+5)=3(x-5)$
$\Leftrightarrow (x-5)(x+5-3)=0$
$\Leftrightarrow (x-5)(x+2)=0$
$\Leftrightarrow x-5=0$ hoặc $x+2=0$
$\Leftrightarrow x=5$ hoặc $x=-2$


Điều kiện:
\(x-1\ne0\Rightarrow x\ne1\)
\(x^3+x\ne0\Leftrightarrow x\ne0\)

Đề số 3.
1.
a,\(4x\left(5x^2-2x+3\right)\)
\(=20x^3-8x^2+12x\)
b.\(\left(x-2\right)\left(x^2-3x+5\right)\)
\(=x^3-3x^2+5x-2x^2+6x-10\)
\(=x^3-5x^2+11x-10\)
c,\(\left(10x^4-5x^3+3x^2\right):5x^2\)
\(=2x^2-x+\dfrac{3}{5}\)
d,\(\left(x^2-12xy+36y^2\right):\left(x-6y\right)\)
\(=\left(x-6y\right)^2:\left(x-6y\right)\)
\(=x-6y\)
2.
a,\(x^2+5x+5xy+25y\)
\(=\left(x^2+5x\right)+\left(5xy+25y\right)\)
\(=x\left(x+5\right)+5y\left(x+5\right)\)
\(=\left(x+5y\right)\left(x+5\right)\)
b,\(x^2-y^2+14x+49\)
\(=\left(x^2+14x+49\right)-y^2\)
\(=\left(x+7\right)^2-y^2\)
\(=\left(x+7-y\right)\left(x+7+y\right)\)
c,\(x^2-24x-25\)
\(=x^2+25x-x-25\)
\(=\left(x^2-x\right)+\left(25x-25\right)\)
\(=x\left(x-1\right)+25\left(x-1\right)\)
\(=\left(x+25\right)\left(x-1\right)\)
3.
a,\(5x\left(x-3\right)-x+3=0\)
\(5x\left(x-3\right)-\left(x-3\right)=0\)
\(\left(5x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-1=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=1\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=3\end{matrix}\right.\)
Vậy \(x=\dfrac{1}{5}\) hoặc \(x=3\)
b.\(3x\left(x-5\right)-\left(x-1\right)\left(2+3x\right)=30\)
\(3x^2-15x-\left(2x+3x^2-2-3x\right)=30\)
\(3x^2-15x-2x-3x^2+2+3x=30\)
\(-14x+2=30\)
\(-14x=28\)
\(x=-2\)
c,\(\left(x+2\right)\left(x+3\right)-\left(x-2\right)\left(x+5\right)=0\)
\(x^2+3x+2x+6-\left(x^2+5x-2x-10\right)=0\)
\(x^2+5x+6-x^2-5x+2x+10=0\)
\(2x+16=0\)
\(2x=-16\)
\(x=-8\)
Mình học chật hình không giúp bạn được.Xin lỗi!

a)tam giác BHA có BI là phân giác(góc ABI=góc HBI) nên \(\dfrac{AI}{IH}=\dfrac{AB}{BH}\Rightarrow AI\cdot BH=AB\cdot IH\)
b)xét tam giác BHA và tam giác BAC có:
góc ABC chung
góc BHA=góc BAC=90 độ
\(\Rightarrow\Delta BHA\infty\Delta BAC\left(g.g\right)\\ \Rightarrow\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow AB^2=BH\cdot BC\)
c)ta có:
theo câu a) \(\dfrac{AI}{IH}=\dfrac{AB}{BH}\Rightarrow\dfrac{IH}{AI}=\dfrac{BH}{AB}\left(1\right)\)
theo câu b) \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\)
ta lại có BD là phân giác góc ABC nên \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{AD}{DC}=\dfrac{BH}{AB}\)(2)
từ (1) và (2)\(\Rightarrow\dfrac{IH}{IA}=\dfrac{AD}{DC}\left(=\dfrac{BH}{AB}\right)\)

Câu 4:
a: ĐKXĐ: \(x\notin\left\{0;-5\right\}\)
b: \(A=\dfrac{x^2+2x}{2\left(x+5\right)}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2}{2x\left(x+5\right)}+\dfrac{2\left(x^2-25\right)}{2x\left(x+5\right)}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+4x^2-5x}{2x\left(x+5\right)}=\dfrac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}\)
\(=\dfrac{x\left(x+5\right)\left(x-1\right)}{2x\left(x+5\right)}=\dfrac{x-1}{2}\)
c: Để A=-3 thì x-1=-6
hay x=-5(loại)

Xét hình thang cân ABCD có:
MA=MB (M là trung điểm AB:gt)
=>MA đối xứng với MB qua MN
AD=BC (do ABCD là htc)
=>AD đối xứng với BC qua MN
ND=NC (N là trung điểm của AC:gt)
=>ND đối xứng với NC qua MN
Do đó tứ giác MADN đối xứng với tứ giác MBCN qua MN
Vậy htc ABCD có một trục đối xứng là MN


 giúp mk nha mờn nhìu ạk
giúp mk nha mờn nhìu ạk










 cac
cac

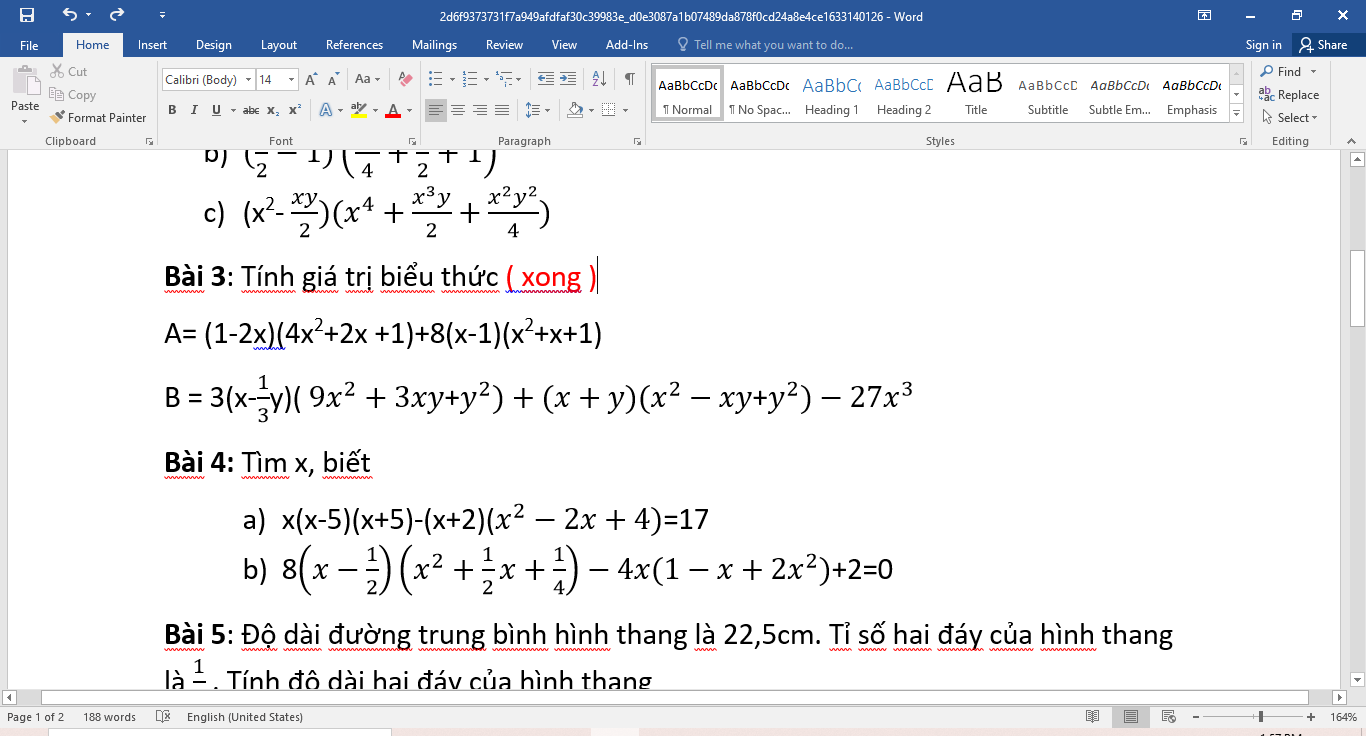
\(3,\\ A=1-8x^3+8x^3-8=-7\\ B=\left(3x-y\right)\left(9x^2+3xy+y^2\right)+x^3+y^3-27x^3\\ B=27x^3-y^3+x^3+y^3-27x^3=x^3\)
Bài 4:
a: Ta có: \(x\left(x-5\right)\left(x+5\right)-\left(x+2\right)\left(x^2-2x+4\right)=17\)
\(\Leftrightarrow x^3-25x-x^3-8=17\)
\(\Leftrightarrow-25x=25\)
hay x=-1
b: Ta có: \(8\left(x-\dfrac{1}{2}\right)\left(x^2+\dfrac{1}{2}x+\dfrac{1}{4}\right)-4x\left(2x^2-x+1\right)+2=0\)
\(\Leftrightarrow8x^3-1-8x^3+4x^2-4x+2=0\)
\(\Leftrightarrow2x-1=0\)
hay \(x=\dfrac{1}{2}\)