
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC
b: Xét ΔAMC và ΔACN có
góc ACM=góc ANC
góc MAC chung
=>ΔAMC đồng dạng với ΔACN
c: ΔAMC đồng dạng với ΔACN
=>AM/AC=AC/AN
=>AC^2=AM*AN=AH*AO

1: góc AHC+góc AKC=180 độ
=>AHCK nội tiếp
2: AHCK nội tiếp
=>góc AHK=góc ACK=1/2*sđ cung AC=góc ABC

a) Ta có: \(Q=\dfrac{3x+\sqrt{9x}-3}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{\sqrt{x}-2}{1-\sqrt{x}}\)
\(=\dfrac{3x+3\sqrt{x}-3-\left(x-1\right)-\left(x-4\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{3x+3\sqrt{x}-3-x+1-x+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+3\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b) Thay \(x=4+2\sqrt{3}\) vào Q, ta được:
\(Q=\dfrac{\sqrt{3}+1+1}{\sqrt{3}+1-1}=\dfrac{2+\sqrt{3}}{\sqrt{3}}=\dfrac{2\sqrt{3}+3}{3}\)
c) Để Q=3 thì \(\sqrt{x}+1=3\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\sqrt{x}=-3-1\)
\(\Leftrightarrow2\sqrt{x}=4\)
hay x=4
d) Để \(Q>\dfrac{1}{2}\) thì \(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}+2-\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}>0\)
\(\Leftrightarrow\sqrt{x}-1>0\)
\(\Leftrightarrow x>1\)
Kết hợp ĐKXĐ, ta được: x>1
e) Để Q nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-1\)
\(\Leftrightarrow2⋮\sqrt{x}-1\)
\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;3\right\}\)
hay \(x\in\left\{0;4;9\right\}\)

\(1,A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\left(x>0;x\ne1;x\right)\\ A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ A=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\left(\sqrt{x}-1\right)=\dfrac{x-1}{\sqrt{x}}\)
\(2,x=2\sqrt{2}+3=\left(\sqrt{2}+1\right)^2\\ \Leftrightarrow A=\dfrac{2\sqrt{2}+3}{\sqrt{2}+1}=\dfrac{\left(2\sqrt{2}+3\right)\left(\sqrt{2}-1\right)}{1}\\ =4\sqrt{2}-2\sqrt{2}+3\sqrt{2}-3=5\sqrt{2}-3\)



Bài I:
1: Thay x=4 vào A, ta được:
\(A=\dfrac{4}{2+1}=\dfrac{4}{3}\)
2: \(B=\dfrac{3}{\sqrt{x}+1}+\dfrac{x+5}{x-1}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{3}{\sqrt{x}+1}+\dfrac{\left(x+5\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{3\left(\sqrt{x}-1\right)+x+5-\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{3\sqrt{x}-3+x-\sqrt{x}+4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
3: P=A*B
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\cdot\dfrac{x}{\sqrt{x}+1}=\dfrac{x}{\sqrt{x}-1}\)
P<=4
=>P-4<=0
=>\(\dfrac{x-4\sqrt{x}+4}{\sqrt{x}-1}< =0\)
=>\(\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}< =0\)
=>\(\sqrt{x}-1< 0\)
=>\(\sqrt{x}< 1\)
=>0<=x<1
Kết hợp ĐKXĐ, ta được: 0<=x<1

a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=4\cdot9=36\)
hay AH=6(cm)
Xét tứ giác AEHD có
\(\widehat{AEH}=90^0\)
\(\widehat{ADH}=90^0\)
\(\widehat{EAD}=90^0\)
Do đó: AEHD là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Suy ra: AH=ED(Hai đường chéo)
mà AH=6cm
nên ED=6cm
Vậy: ED=6cm
b) Gọi G là giao điểm của AH và DE
=> GA=GD=GE=GH
hay ΔGHD cân tại G
\(\Leftrightarrow\widehat{GHD}=\widehat{GDH}\)
\(\Leftrightarrow\widehat{MDH}=\widehat{MHD}\)(2)
hay ΔMDH cân tại M
Suy ra: MH=MD(1)
Ta có: \(\widehat{MDH}+\widehat{MDB}=90^0\)(3)
\(\widehat{MHD}+\widehat{MBD}=90^0\)(4)
Từ (2), (3) và (4) suy ra \(\widehat{MDB}=\widehat{MBD}\)
hay ΔMDB cân tại M
Suy ra: MD=MB(5)
Từ (1) và (5) suy ra MH=MB
mà M nằm giữa H và B
nên M là trung điểm của HB
CM tương tự, ta được: NH=NC
hay N là trung điểm của CH
Ta có: HB+HC=BC(H nằm giữa B và C)
nên 2NH+2MH=BC
\(\Leftrightarrow MN=\dfrac{1}{2}BC\)(đpcm)
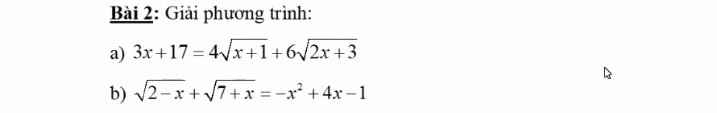


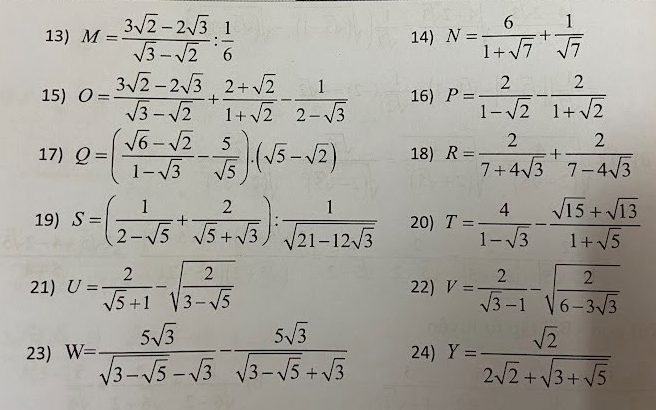
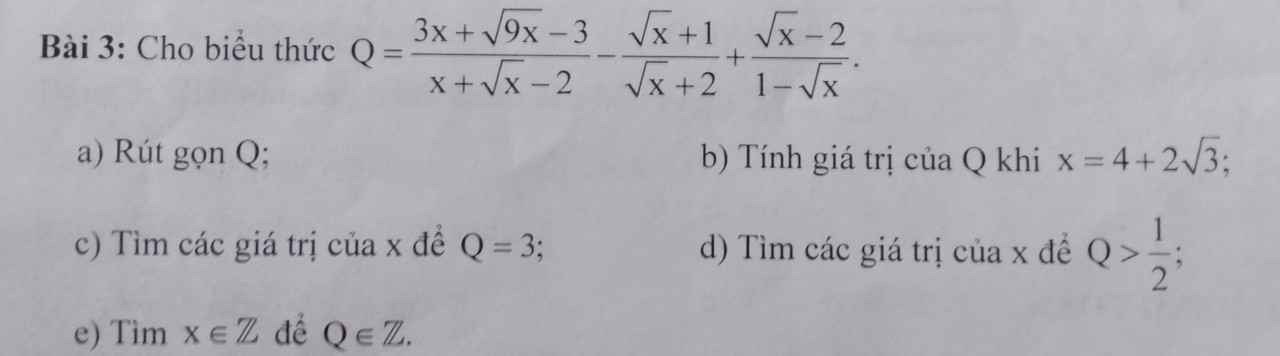 giúp mình vs mình đg cần gấp
giúp mình vs mình đg cần gấp 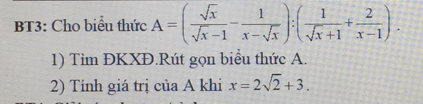
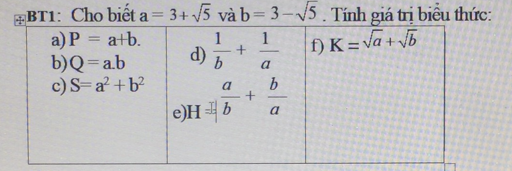

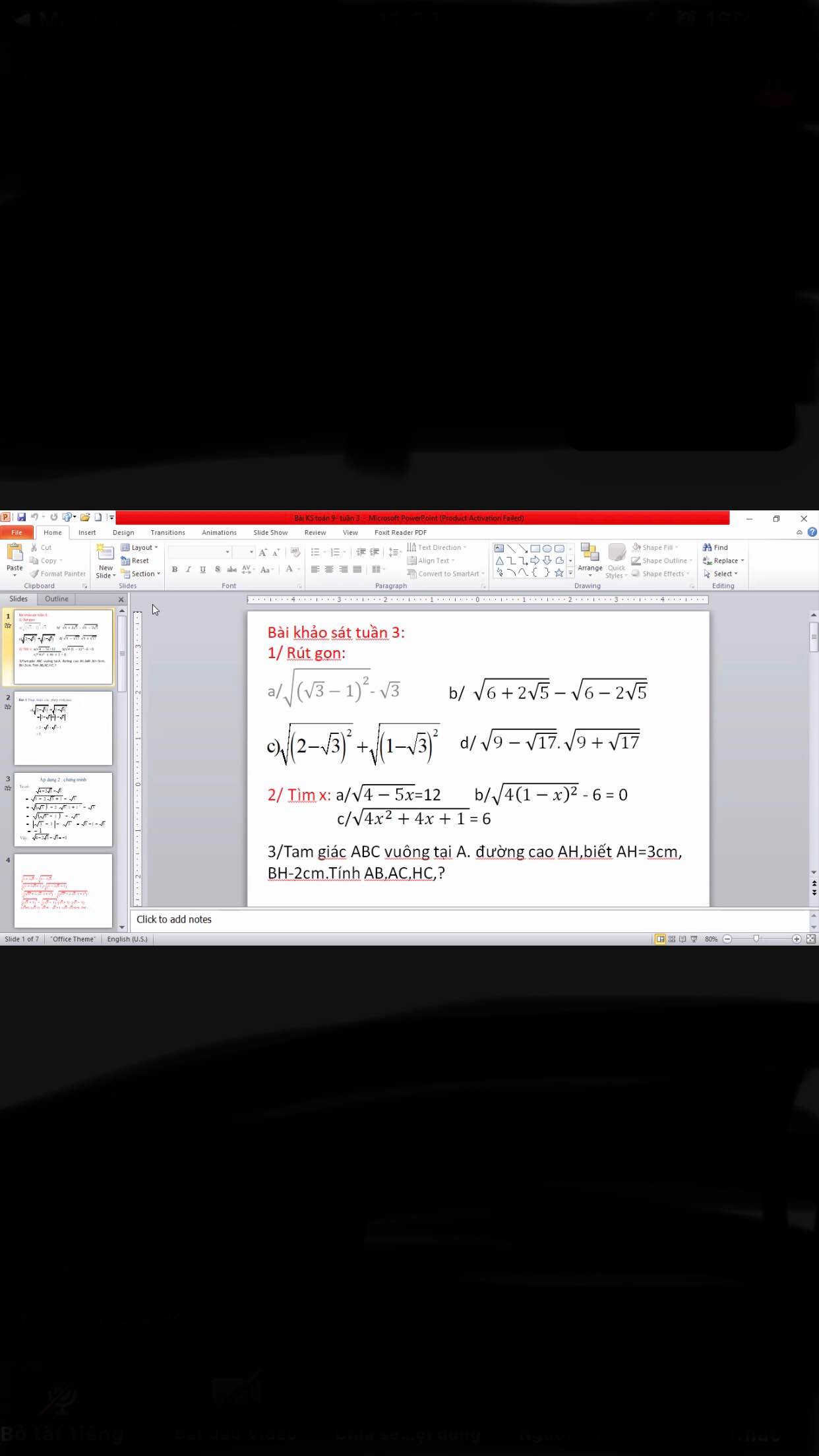


a.
ĐKXĐ: \(x\ge-1\)
\(\Leftrightarrow\left(x+1-4\sqrt{x+1}+4\right)+\left(2x+3-6\sqrt{2x+3}+9\right)=0\)
\(\Leftrightarrow\left(\sqrt{x+1}-2\right)^2+\left(\sqrt{2x+3}-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x+1}-2=0\\\sqrt{2x+3}-3=0\end{matrix}\right.\)
\(\Leftrightarrow x=3\)
b.
Ta có:
\(VT=\sqrt{2-x}+\sqrt{7+x}\ge\sqrt{2-x+7+x}=3\)
\(VP=-\left(x-2\right)^2+3\le3\)
Đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}\left(2-x\right)\left(7+x\right)=0\\x-2=0\end{matrix}\right.\) \(\Leftrightarrow x=2\)