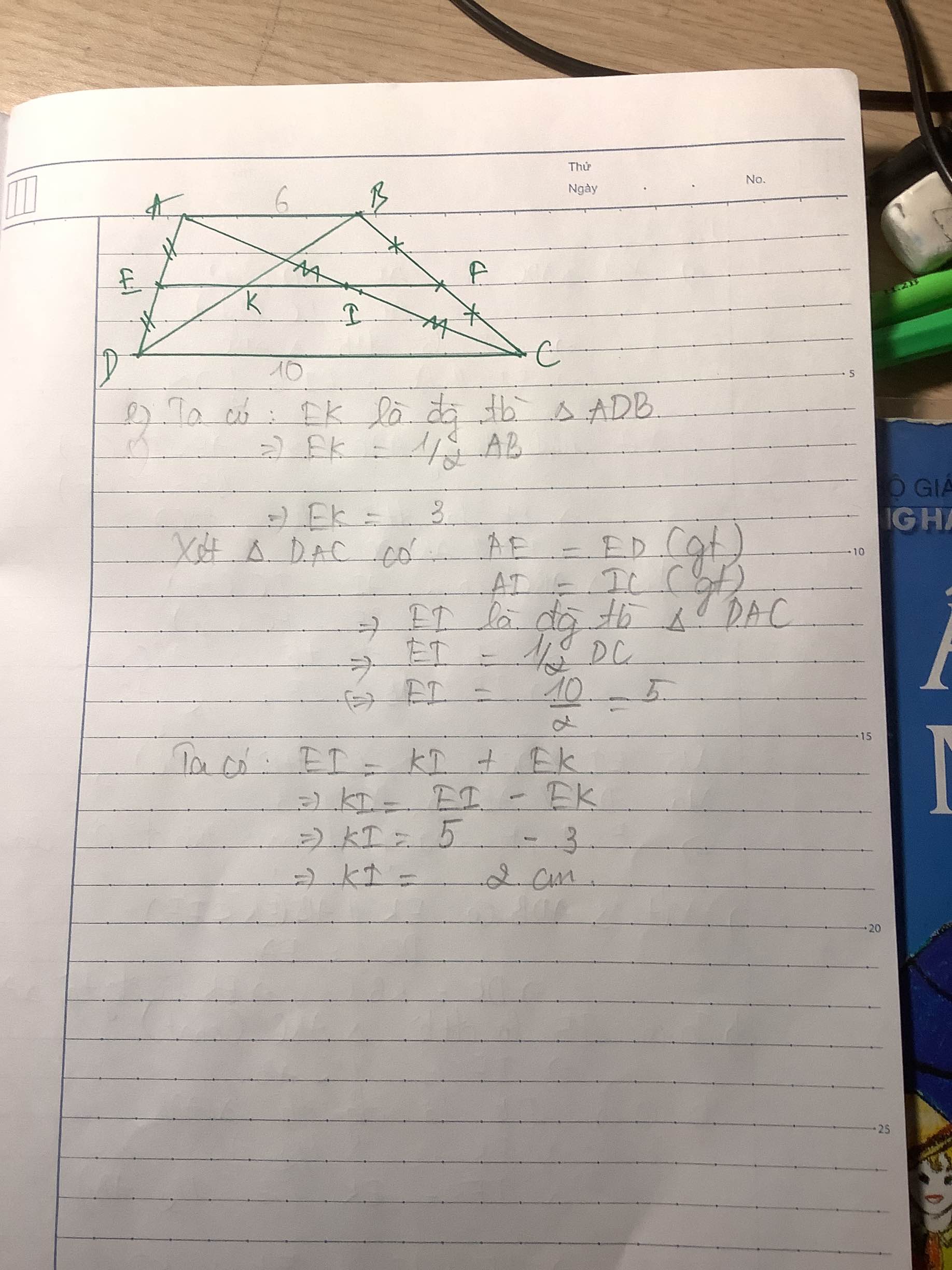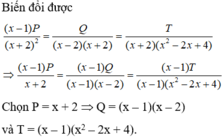K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
1
30 tháng 8 2021
1: \(\left(x+1\right)^3=x^3+3x^2+3x+1\)
2: \(\left(x-1\right)^3=x^3-3x^2+3x-1\)
3: \(x^3+1=\left(x+1\right)\left(x^2-x+1\right)\)
4: \(x^3-1=\left(x-1\right)\left(x^2+x+1\right)\)
5: \(\left(x+2\right)^3=x^3+6x^2+12x+8\)
23 tháng 8 2021
a: Xét ΔADC có
E là trung điểm của AD
I là trung điểm của AC
Do đó: EI là đường trung bình của ΔADC
Suy ra: EI//DC
Suy ra: EI//DC
Xét hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: EF//AB//CD
b: Ta có: EI//DC
EF//DC
mà EI và EF có điểm chung là E
nên E,I,F thẳng hàng
25 tháng 8 2021
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
HN
1
17 tháng 8 2021
Bài 13:
a: Ta có: \(AE=EB=\dfrac{AB}{2}\)
\(AD=DC=\dfrac{AC}{2}\)
mà AB=AC
nên AE=EB=AD=DC
Xét ΔAED có AE=AD
nên ΔADE cân tại A
b: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{BAD}\) chung
AD=AE
Do đó: ΔABD=ΔACE
c: Xét ΔABC có
\(\dfrac{AE}{EB}=\dfrac{AD}{DC}\left(=1\right)\)
Do đó: DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà BD=CE
nên BEDC là hình thang cân
7 tháng 6 2021
`((x-1)P)/(x+2)^2=Q/((x-2)(x+2))=T/((x+2)(x^2-2x+4))`
Nhân 2 vế với `x+2 ne 0` ta có:
`((x-1)P)/(x+2)=Q/(x-2)=T/(x^2-2x+4)`
Nhân cả tử và mẫu với `x-1 ne 0` ta có:
`((x-1)P)/(x+2)=((x-1)Q)/((x-1)(x-2))=((x-1)T)/((x-1)(x^2-2x+4))`