
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: \(\dfrac{15x}{7y^3}\cdot\dfrac{2y^2}{x^2}\)
\(=\dfrac{15x\cdot2y^2}{7y^3\cdot x^2}=\dfrac{30xy^2}{7x^2y^3}=\dfrac{30}{7xy}\)
2: \(\dfrac{6x^3}{7y^4}\cdot\dfrac{35y^2}{24x}\)
\(=\dfrac{6x^3}{24x}\cdot\dfrac{35y^2}{7y^4}\)
\(=\dfrac{x^2}{4}\cdot\dfrac{5}{y^2}=\dfrac{5x^2}{4y^2}\)
3: \(\dfrac{4y^2}{x^4}\cdot\dfrac{-3x^2}{8y}\)
\(=\dfrac{4y^2}{8y}\cdot\dfrac{-3x^2}{x^4}=\dfrac{y}{2}\cdot\dfrac{-3}{x^2}=\dfrac{-3y}{2x^2}\)
4: \(\dfrac{-18y^3}{25x^4}:\dfrac{9y^3}{-15x^2}\)
\(=\dfrac{18y^3}{25x^4}\cdot\dfrac{15x^2}{9y^3}\)
\(=\dfrac{18y^3}{9y^3}\cdot\dfrac{15x^2}{25x^4}=2\cdot\dfrac{3}{5x^2}=\dfrac{6}{5x^2}\)
5: \(\dfrac{8y^2}{9x^2}:\dfrac{4y}{3x^2}\)
\(=\dfrac{8y^2}{9x^2}\cdot\dfrac{3x^2}{4y}=\dfrac{8y^2}{4y}\cdot\dfrac{3x^2}{9x^2}=\dfrac{1}{3}\cdot2y=\dfrac{2y}{3}\)
6: \(\dfrac{-20x}{3y^2}:\dfrac{-4x^3}{5y}\)
\(=\dfrac{20x}{3y^2}:\dfrac{4x^3}{5y}\)
\(=\dfrac{20x}{3y^2}\cdot\dfrac{5y}{4x^3}=\dfrac{20x}{4x^3}\cdot\dfrac{5y}{3y^2}=\dfrac{5}{3y}\cdot\dfrac{5}{x^2}=\dfrac{25}{3x^2y}\)
7: \(\dfrac{\left(x+4\right)^2}{4x+12}:\dfrac{x+4}{3x+9}\)
\(=\dfrac{\left(x+4\right)^2}{4\left(x+3\right)}:\dfrac{x+4}{3\left(x+3\right)}\)
\(=\dfrac{\left(x+4\right)^2}{4\left(x+3\right)}\cdot\dfrac{3\left(x+3\right)}{x+4}=\dfrac{3\left(x+4\right)}{4}\)
8: \(\dfrac{5x+10}{4x-8}\cdot\dfrac{4-2x}{x+2}\)
\(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}\)
\(=\dfrac{5\cdot\left(-2\right)}{4}=-\dfrac{10}{4}=-\dfrac{5}{2}\)
9: \(\dfrac{x^2-36}{2x+10}\cdot\dfrac{3}{6-x}\)
\(=\dfrac{\left(x-6\right)\left(x+6\right)}{2\left(x+5\right)}\cdot\dfrac{-3}{x-6}\)
\(=\dfrac{-3\left(x+6\right)}{2\left(x+5\right)}\)
10: \(\dfrac{x^2-4}{x^2-x}:\dfrac{x^2+2x}{x-1}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-1\right)}\cdot\dfrac{x-1}{x\left(x+2\right)}\)
\(=\dfrac{\left(x-2\right)}{x^2\left(x+2\right)}\)

e) Ta có: \(x^3-4x-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2\right)-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2-14\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=12\end{matrix}\right.\)
e)x3-4x+14x(x-2)=0
⇔ x(x2-4)+14x(x-2)=0
⇔ x(x-2)(x+2)+14x(x-2)=0
⇔ (x-2)(x2+2x+14x)=0
⇔ x(x-2)(x+16)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-2=0\\x+16=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=2\\x=-16\end{matrix}\right.\)
g)x2(x+1)-x(x+1)+x(x-1)=0
⇔ (x+1)(x2-x)+x(x-1)=0
⇔ x(x+1)(x-1)+x(x-1)=0
⇔ x(x-1)(x+2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=1\\x=-2\end{matrix}\right.\)

\(\left(\dfrac{1}{8}\right)^9\cdot8^9-\left(\dfrac{3}{4}-2x\right)^2=\dfrac{41}{9}-\dfrac{72^2}{36^2}\\ \Rightarrow\left(\dfrac{1}{8}\cdot8\right)^9-\left(\dfrac{3}{4}-2x\right)^2=\dfrac{41}{9}-\left(\dfrac{72}{36}\right)^2\\ \Rightarrow1^9-\left(\dfrac{3}{4}-2x\right)^2=\dfrac{41}{9}-2^2=\dfrac{5}{9}\\ \Rightarrow\left(\dfrac{3}{4}-2x\right)^2=1-\dfrac{5}{9}=\dfrac{4}{9}\\ \Rightarrow\left[{}\begin{matrix}\dfrac{3}{4}-2x=\dfrac{2}{3}\\2x-\dfrac{3}{4}=\dfrac{2}{3}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=\dfrac{1}{12}\\2x=\dfrac{17}{12}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{24}\\x=\dfrac{17}{24}\end{matrix}\right.\)

a, \(\dfrac{2^3-x^3}{x\left(x^2+2x+4\right)}\) = \(\dfrac{\left(2-x\right)\left(x^2+2x+4\right)}{x\left(x^2+2x+4\right)}\) = \(\dfrac{2-x}{x}\)=\(\dfrac{x-2}{-x}\)(đpcm)
b, \(\dfrac{-3x\left(x-y\right)}{y^2-x^2}\) (\(x\) \(\ne\) \(\pm\) y)
= \(\dfrac{-3x\left(x-y\right)}{\left(y-x\right)\left(y+x\right)}\)
= \(\dfrac{3x\left(y-x\right)}{\left(y-x\right)\left(y+x\right)}\)
= \(\dfrac{3x}{x+y}\) (đpcm)

Câu 12:
b: \(Q=\dfrac{x^2-1+2x+1}{x\left(x+1\right)}=\dfrac{x+2}{x+1}\)


Bài 2:
1: ĐKXĐ: x<>1
\(\dfrac{x}{x-1}+\dfrac{1}{1-x}\)
\(=\dfrac{x}{x-1}-\dfrac{1}{x-1}\)
\(=\dfrac{x-1}{x-1}=1\)
2: ĐKXĐ: x<>3/2
\(\dfrac{11x}{2x-3}-\dfrac{x-18}{3-2x}\)
\(=\dfrac{11x}{2x-3}+\dfrac{x-18}{2x-3}\)
\(=\dfrac{11x+x-18}{2x-3}=\dfrac{12x-18}{2x-3}\)
\(=\dfrac{6\left(2x-3\right)}{2x-3}\)
=6
3: ĐKXĐ: x<>1/2
\(\dfrac{4x+5}{2x-1}+\dfrac{5-9x}{1-2x}\)
\(=\dfrac{4x+5}{2x-1}+\dfrac{9x-5}{2x-1}\)
\(=\dfrac{4x+5+9x-5}{2x-1}=\dfrac{13x}{2x-1}\)
4: ĐKXĐ: x<>2/5
\(\dfrac{2x-7}{10x-4}-\dfrac{3x+5}{4-10x}\)
\(=\dfrac{2x-7}{10x-4}+\dfrac{3x+5}{10x-4}\)
\(=\dfrac{2x-7+3x+5}{10x-4}=\dfrac{5x-2}{10x-4}=\dfrac{1}{2}\)
5: ĐKXĐ: \(x\ne\pm y\)
\(\dfrac{xy}{x^2-y^2}-\dfrac{x^2}{y^2-x^2}\)
\(=\dfrac{xy}{x^2-y^2}+\dfrac{x^2}{x^2-y^2}\)
\(=\dfrac{x\left(x+y\right)}{\left(x-y\right)\left(x+y\right)}=\dfrac{x}{x-y}\)
6: ĐKXĐ: \(x\notin\left\{0;7\right\}\)
\(\dfrac{4x+13}{5x\left(x-7\right)}-\dfrac{x-48}{5x\left(7-x\right)}\)
\(=\dfrac{4x+13}{5x\left(x-7\right)}+\dfrac{x-48}{5x\left(x-7\right)}\)
\(=\dfrac{4x+13+x-48}{5x\left(x-7\right)}\)
\(=\dfrac{5x-35}{x\left(5x-35\right)}=\dfrac{1}{x}\)
7: ĐKXĐ: \(x\ne1\)
\(\dfrac{x+2}{x-1}-\dfrac{x-9}{1-x}-\dfrac{x-9}{1-x}\)
\(=\dfrac{x+2}{x-1}+\dfrac{x-9}{x-1}+\dfrac{x-9}{x-1}\)
\(=\dfrac{x+2+x-9+x-9}{x-1}=\dfrac{3x-16}{x-1}\)
8: ĐKXĐ:x<>1
\(\dfrac{2x^2-x}{x-1}+\dfrac{x+1}{1-x}+\dfrac{2-x^2}{x-1}\)
\(=\dfrac{2x^2-x}{x-1}-\dfrac{x+1}{x-1}+\dfrac{2-x^2}{x-1}\)
\(=\dfrac{2x^2-x-x-1+2-x^2}{x-1}=\dfrac{x^2-2x+1}{x-1}\)
=x-1
9: ĐKXĐ: x<>3
\(\dfrac{4-x^2}{x-3}+\dfrac{2x-x^2}{3-x}+\dfrac{5-4x}{x-3}\)
\(=\dfrac{4-x^2}{x-3}+\dfrac{x^2-2x}{x-3}+\dfrac{5-4x}{x-3}\)
\(=\dfrac{4-x^2+x^2-2x+5-4x}{x-3}=\dfrac{-6x+9}{x-3}\)
10: ĐKXĐ: x<>5
\(\dfrac{x+1}{x-5}+\dfrac{x-18}{5-x}+\dfrac{x+2}{x-5}\)
\(=\dfrac{x+1}{x-5}-\dfrac{x-18}{x-5}+\dfrac{x+2}{x-5}\)
\(=\dfrac{x+1-x+18+x+2}{x-5}=\dfrac{3x-15}{x-5}=3\)

a) Xét ΔAEN có
D là trung điểm của AE
DM//EN
Do đó: M là trung điểm của AN
b) Hình thang DMCB có
E là trung điểm của DB
EN//DM//CB
Do đó: N là trung điểm của MC
Suy ra: MN=NC
mà MN=AM
nên AM=MN=NC
c) Xét hình thang DMCB có
E là trung điểm của DB
N là trung điểm của MC
Do đó: EN là đường trung bình của hình thang DMCB
Suy ra: \(EN=\dfrac{DM+CB}{2}\)
hay \(2EN=DM+BC\)
a/ Xét △AEN có:
- \(DM\text{//}EN\left(gt\right)\)
- D là trung điểm của AE \(\left(AD=AE\right)\)
=> DM là đường trung bình của △AEN. Vậy: M là trung điểm của AN (đpcm)
b/ Tứ giác BDMC có \(EN\text{ // }BC\left(gt\right)\) => Tứ giác BDMC là hình thang
Hình thang BDMC có:
- \(EN\text{ // }BC\left(gt\right)\)
- E là trung điểm của DB \(\left(DE=EB\right)\)
=> EN là đường trung bình của hình thang BDMC => N là trung điểm của MC hay \(MN=NC\)
- Mà \(AM=MN\left(cmt\right)\)
Vậy: \(AM=MN=NC\left(đpcm\right)\)
c/ - Ta có: EN là đường trung bình của hình thang BDMC (cmt)
=> \(EN=\dfrac{DM+BC}{2}\)
Vậy: \(2EN=2\cdot\dfrac{DN+BC}{2}=DN+BC\left(đpcm\right)\)

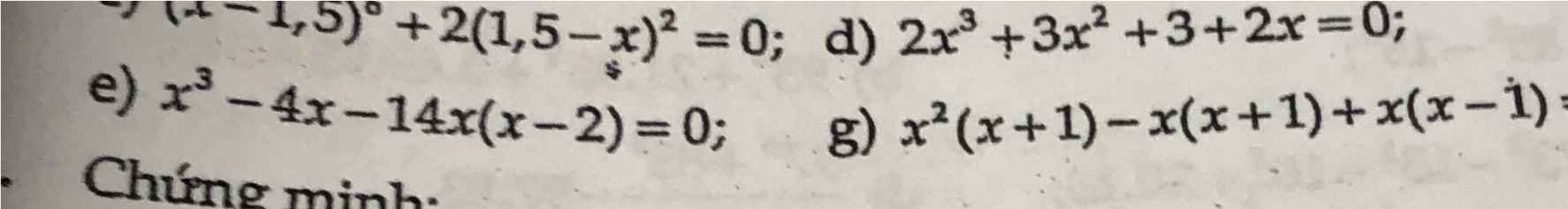
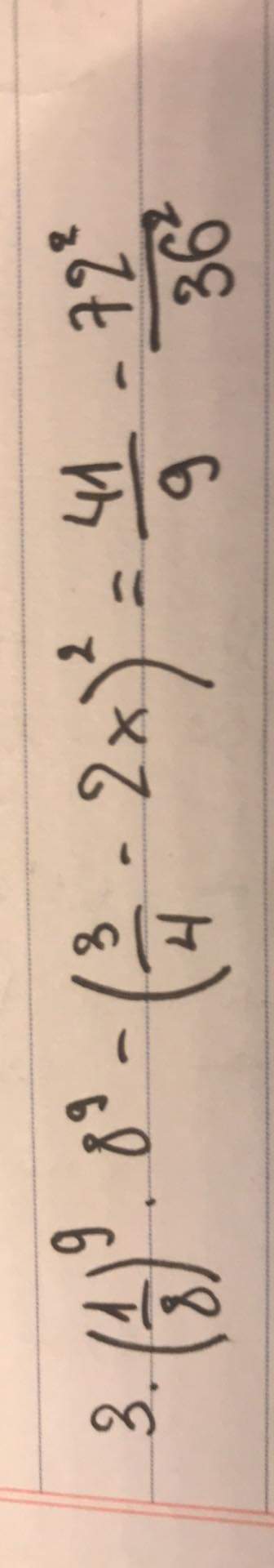
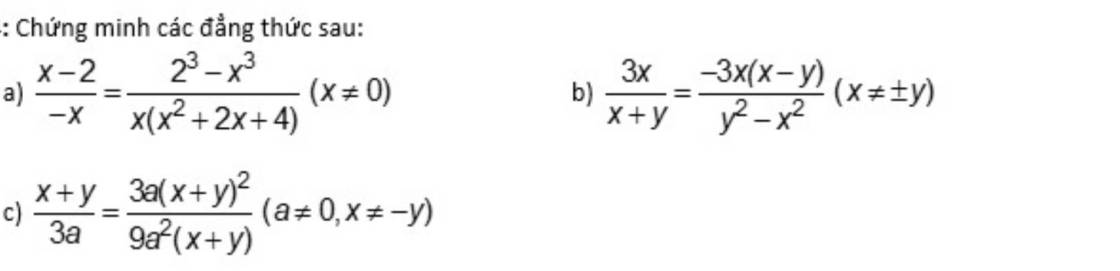
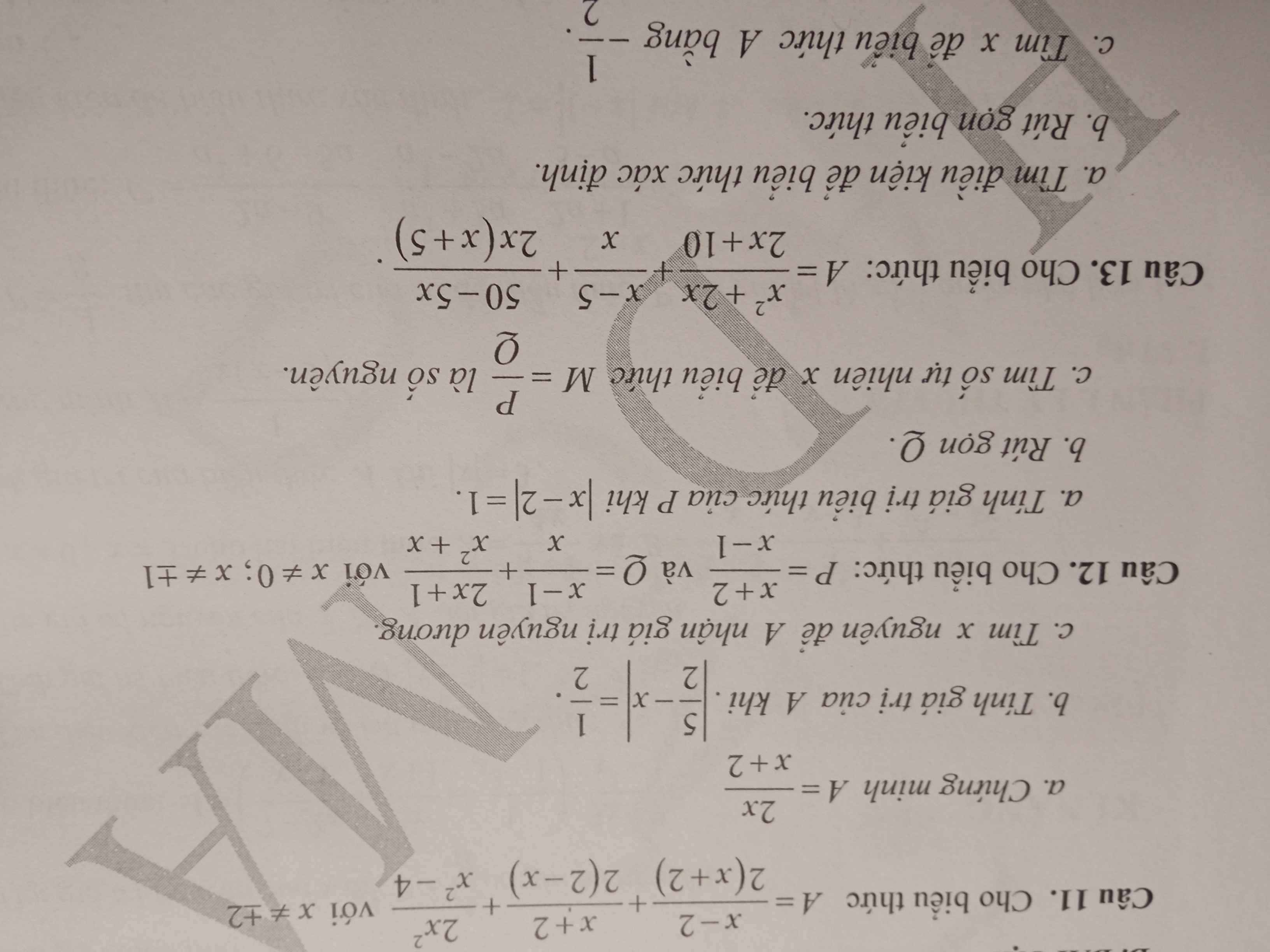 giải giúp mình bài này nha
giải giúp mình bài này nha
