Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a: Xét ΔABC có
BI,CI là các đường phân giác
BI cắt CI tại I
Do đó: I là tâm đường tròn nội tiếp ΔABC
b: Ta có: \(\widehat{DIB}=\widehat{IBC}\)(hai góc so le trong, DI//BC)
\(\widehat{DBI}=\widehat{IBC}\)(BI là phân giác của góc DBC)
Do đó: \(\widehat{DIB}=\widehat{DBI}\)
=>ΔDIB cân tại D
c: Ta có: \(\widehat{EIC}=\widehat{ICB}\)(hai góc so le trong, EI//BC)
\(\widehat{ECI}=\widehat{ICB}\)(CI là phân giác của góc ECB)
Do đó: \(\widehat{EIC}=\widehat{ECI}\)
=>ΔEIC cân tại E
d: Ta có: ΔDIB cân tại D
=>DB=DI
Ta có: ΔEIC cân tại E
=>EI=EC
Ta có: DI+IE=DE
mà DI=DB
và EC=EI
nên DB+EC=DE
Bài 1:
a: Xét ΔABC có
BE,CF là các đường phân giác
BE cắt CF tại I
Do đó: I là tâm đường tròn nội tiếp ΔABC
=>AI là phân giác của góc BAC
b: ta có: \(\widehat{ABE}=\widehat{CBE}=\dfrac{\widehat{ABC}}{2}\)(BE là phân giác của góc ABC)
\(\widehat{ACF}=\widehat{FCB}=\dfrac{\widehat{ACB}}{2}\)(CF là phân giác của góc ACB)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABE}=\widehat{EBC}=\widehat{ACF}=\widehat{FCB}\)
c: ta có: \(\widehat{EBC}=\widehat{FCB}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
d: Xét ΔABE và ΔACF có
\(\widehat{ABE}=\widehat{ACF}\)
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
=>BE=CF
e:
Ta có: ΔAEB=ΔAFC
=>AE=AF
Ta có: AE+EC+AC
AF+FB=AB
mà AE=AF
và AC=AB
nên EC=FB
Xét ΔFIB và ΔEIC có
FB=EC
\(\widehat{FBI}=\widehat{ECI}\)
BI=CI
Do đó: ΔFIB=ΔEIC

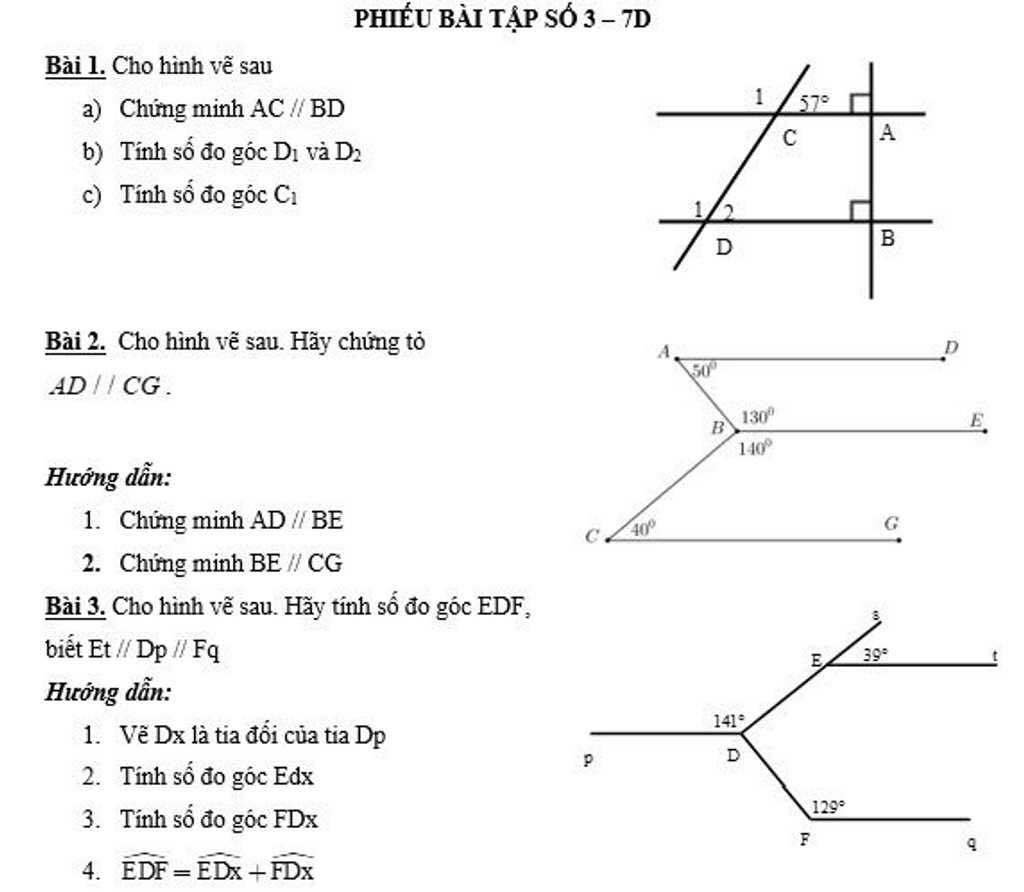
\(1,\\ a,\left\{{}\begin{matrix}AC\perp AB\\BD\perp AB\end{matrix}\right.\Rightarrow AC//BD\\ b,AC//BD\Rightarrow\widehat{D_2}=\widehat{C_1}=57^0\left(đồng.vị\right)\\ \widehat{D_2}+\widehat{D_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{D_1}=180^0-57^0=123^0\\ c,AC//BD\Rightarrow\widehat{D_1}=\widehat{C_1}=123^0\left(đồng.vị\right)\)
\(2,\\ \widehat{DAB}+\widehat{ABE}=50^0+130^0=180^0\)
Mà 2 góc này ở vị trí TCP nên AD//BE (1)
\(\widehat{EBC}+\widehat{BCG}=140^0+40^0=180^0\)
Mà 2 góc này ở vị trí TCP nên BE//CG (2)
Từ (1)(2) ta được AD//CG

Bài 9:
a: Xét ΔAMD vuông tại M và ΔAMI vuông tại M có
AM chung
MD=MI
Do đó: ΔAMD=ΔAMI
Xét ΔAND vuông tại N và ΔANK vuông tại N có
AN chung
ND=NK
Do đó: ΔAND=ΔANK
b: ta có: ΔAMD=ΔAMI
=>\(\widehat{MAD}=\widehat{MAI}\)
=>\(\widehat{DAB}=\widehat{IAB}\)
mà tia AB nằm giữa hai tia AD,AI
nên AB là phân giác của góc DAI
=>\(\widehat{DAI}=2\cdot\widehat{DAB}\)
Ta có: ΔAND=ΔANK
=>\(\widehat{DAN}=\widehat{KAN}\)
=>\(\widehat{DAC}=\widehat{KAC}\)
mà tia AC nằm giữa hai tia AD,AK
nên AC là phân giác của góc DAK
=>\(\widehat{DAK}=2\cdot\widehat{DAC}\)
Ta có: \(\widehat{DAK}+\widehat{DAI}=\widehat{KAI}\)
=>\(\widehat{KAI}=2\cdot\left(\widehat{DAB}+\widehat{DAC}\right)\)
=>\(\widehat{KAI}=2\cdot\widehat{BAC}=180^0\)
=>K,A,I thẳng hàng
c: Ta có: AD=AI(ΔADM=ΔAIM)
AD=AK(ΔADN=ΔAKN)
Do đó: AI=AK
mà K,A,I thẳng hàng
nên A là trung điểm của KI
d: Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
=>AMDN là hình chữ nhật
Hình chữ nhật AMDN có AD là phân giác của góc MAN
nên AMDN là hình vuông
=>DA là phân giác của góc NDM
=>DA là phân giác của góc KDI
Xét ΔDKI có
DA là đường trung tuyến
DA là đường phân giác
Do đó: ΔDKI cân tại D
Ta có: ΔDKI cân tại D
mà DA là đường trung tuyến
nên DA\(\perp\)KI

a: Ta có: \(\left|x+\dfrac{1}{2}\right|\ge0\forall x\)
\(\left|y-\dfrac{3}{4}\right|\ge0\forall y\)
\(\left|z-1\right|\ge0\forall z\)
Do đó: \(\left|x+\dfrac{1}{2}\right|+\left|y-\dfrac{3}{4}\right|+\left|z-1\right|\ge0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left(x,y,z\right)=\left(-\dfrac{1}{2};\dfrac{3}{4};1\right)\)


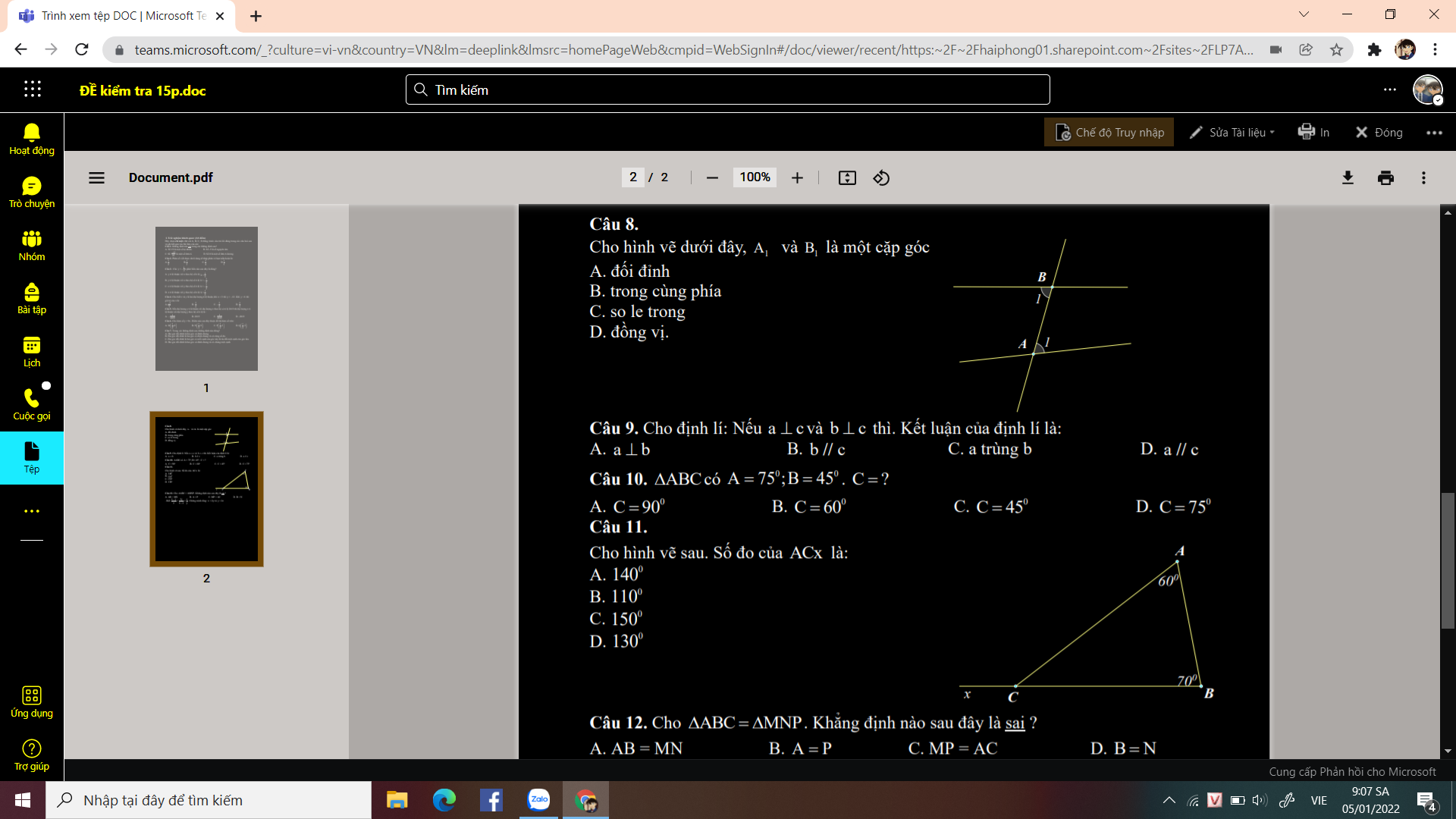
\(\text{8.C.So le trong}\)
\(\text{9.C.a trùng b}\)
\(\text{10.B.}60^0\)
\(\text{11.C.}150^0\)
\(\text{12.B.A=P}\)


 Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi
Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi



Bài nào ạ. Ảnh bị lỗi.