
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : a song song với b
=> Góc A = Góc B = 90độ
Hay x = 90 độ
=> Góc D + Góc C = 180độ ( 2 góc trong cùng phía )
=> y + 130 độ = 180 độ
=> y = 50 độ
Vẽ Cx song song với Am(1), ta được :
=> Góc mAC + Góc ACx = 180 độ
=> Góc mAC + Góc BCA + Góc BCx = 180 độ
Hay Góc BCx = 180 độ - 45 độ - 60 độ = 75 độ
Vì Góc nBC + Góc BCx = 180 độ ( 75 độ + 105 độ = 180 độ )
Mà Góc nBC và Góc BCx là 2 góc trong cùng phía
Nên ta được Bn song song với Cx (2)
Từ (1) và (2) => Bn song song với Am

Bài 1:
x y m B A C 1 1 2 1
Qua B, vẽ tia Bm sao cho Bm // Ax
Bm // Ax ( cách vẽ ) => góc A1 + góc B1 = 180o ( trong cùng phía )
Mà góc A1 = 140o ( giả thiết ) => góc B1 = 40o
Ta có: góc B1 + góc B2 = góc ABC
Mà góc ABC = 70o ( giả thiết ); góc B1 = 40o ( chứng minh trên )
=> góc B2 = 30o
Ta có: góc B2 + góc C1 = 30o + 150o = 180o
Mà hai góc này ở vị trí trong cùng phía
=> Bm // Cy ( dấu hiệu nhận biết 2 đường thẳng song song )
Ta lại có:
Ax // Bm ( cách vẽ ); Cy // Bm ( chứng minh trên )
=> Ax // Cy ( tính chất 3 quan hệ từ vuông góc đến song song ) ( đpcm )
Bài 3:
A B C F E G N M H 1 2
a) Chứng minh AH < \(\dfrac{1}{2}\) ( AB + AC )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AB ( quan hệ giữa đường vuông góc và đường xiên ) ( 1 )
+) Vì AH vuông góc với BC ( giả thiết )
=> AH < AC ( quan hệ giữa đường vuông góc và đường xiên ) ( 2 )
+) Từ ( 1 ) và ( 2 ) => AH + AH < AB + AC
=> 2 . AH < AB + AC
=> AH < \(\dfrac{1}{2}\) ( AB + AC ) ( đpcm )
b) Chứng minh EF = BC
+) Vì BM là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{BG}{BM}=\dfrac{2}{3}\)
=> \(\dfrac{MG}{BG}=\dfrac{1}{2}\)
=> 2 . MG = BG
Mà EM = MG ( do BM là đường trung tuyến của tam giác ABC )
=> EM + MG = BG => EG = BG
+) Vì CN là đường trung tuyến của tam giác ABC ( giả thiết )
=> \(\dfrac{CG}{CN}=\dfrac{2}{3}\)
=> \(\dfrac{GN}{CG}=\dfrac{1}{2}\)
=> 2 . GN = CG
Mà FN = GN ( do CN là đường trung tuyến của tam giác ABC )
=> FN + GN = CG => FG = CG
Góc G1 = góc G2 ( đối đỉnh )
Xét tam giác FEG và tam giác CBG có:
FG = CG ( chứng minh trên )
EG = BG ( chứng minh trên )
Góc G1 = góc G2 ( chứng minh trên )
=> tam giác FEG = tam giác CBG ( c.g.c )
=> EF = BC ( 2 cạnh tương ứng ) ( đpcm )



Bài 1:
A B C . . / D E F / // // x x
a) Xét \(\Delta AED\) và \(\Delta CEF\)có:
AE = EC (gt)
\(\widehat{AED}=\widehat{CEF}\left(đđ\right)\)
DE = EF (gt)
Do đó: \(\Delta AED=\Delta CEF\left(c-g-c\right)\)
=> AD = CF (hai cạnh tương ứng)
mà AD = DB (D là trung điểm của BA)
=> CF = DB
b) Vì \(\Delta AED=\Delta CEF\left(c-g-c\right)\)
=> \(\widehat{DAE}=\widehat{FCE}\) (hai cạnh tương ứng)
=> DA // CF
mà D nằm giữa đoạn thẳng AB (D là trung điểm của AB)
=> DB // CF
=> \(\widehat{BDC}=\widehat{FCD}\left(soletrong\right)\)
Xét \(\Delta BDC\) và \(\Delta FCD\) có:
DC (chung)
\(\widehat{BDC}=\widehat{FCD}\left(cmt\right)\)
BD = CF (cmt)
Do đó: \(\Delta BDC=\Delta FCD\left(c-g-c\right)\)
c) Vì \(\Delta BDC=\Delta FCD\left(cmt\right)\)
=> \(\widehat{BCD}=\widehat{FCD}\) (hai cạnh tương ứng)
=> DF // BC (soletrong)
hay DE // BC
Vì \(\Delta BDC=\Delta FCD\left(cmt\right)\)
=> DF = BC (hai cạnh tương ứng)
mà \(DE=\dfrac{1}{2}DF\) (D là trung điểm của DF)
=> \(DE=\dfrac{1}{2}BC\)


a: \(\widehat{B}=\widehat{Q}=55^0\)
ta có: ΔABC=ΔPQR
nên \(\widehat{A}=\widehat{P};\widehat{C}=R\)
=>\(3\cdot\widehat{P}=2\cdot\widehat{R}\)
\(\Leftrightarrow\widehat{P}=\dfrac{2}{3}\widehat{R}\)
\(\widehat{P}+\widehat{R}=180^0-55^0=125^0\)
\(\widehat{P}=125^0\cdot\dfrac{2}{5}=50^0\)
\(\widehat{R}=125^0-50^0=75^0\)
b: Ta có: ΔABC=ΔGIK
nên AB=GI; BC=IK; AC=GK
=>AB:BC:AC=GI:IK:GK=2:3:4 và CABC=36(cm)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{2}=\dfrac{BC}{3}=\dfrac{AC}{4}=\dfrac{AB+AC+BC}{2+3+4}=\dfrac{36}{9}=4\)
Do đó: AB=8cm; BC=12cm; AC=16cm

a) \(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{99.101}\)
\(=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{99}-\frac{1}{101}\)
\(=1-\frac{1}{101}=\frac{100}{101}\)
b) \(\frac{4}{3.5}+\frac{4}{5.7}+\frac{4}{7.9}+...+\frac{4}{97.99}\)
\(=2\left(\frac{2}{3.5}+\frac{2}{5.7}+\frac{2}{7.9}+...+\frac{2}{97.99}\right)\)
\(=2\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+...+\frac{1}{97}-\frac{1}{99}\right)\)
\(=2\left(\frac{1}{3}-\frac{1}{99}\right)\)
\(=2.\frac{32}{99}=\frac{64}{99}\)

mik cx muốn giúp lắm nhưng mik học c3 rồi ko nhớ cách cấp 2 :))
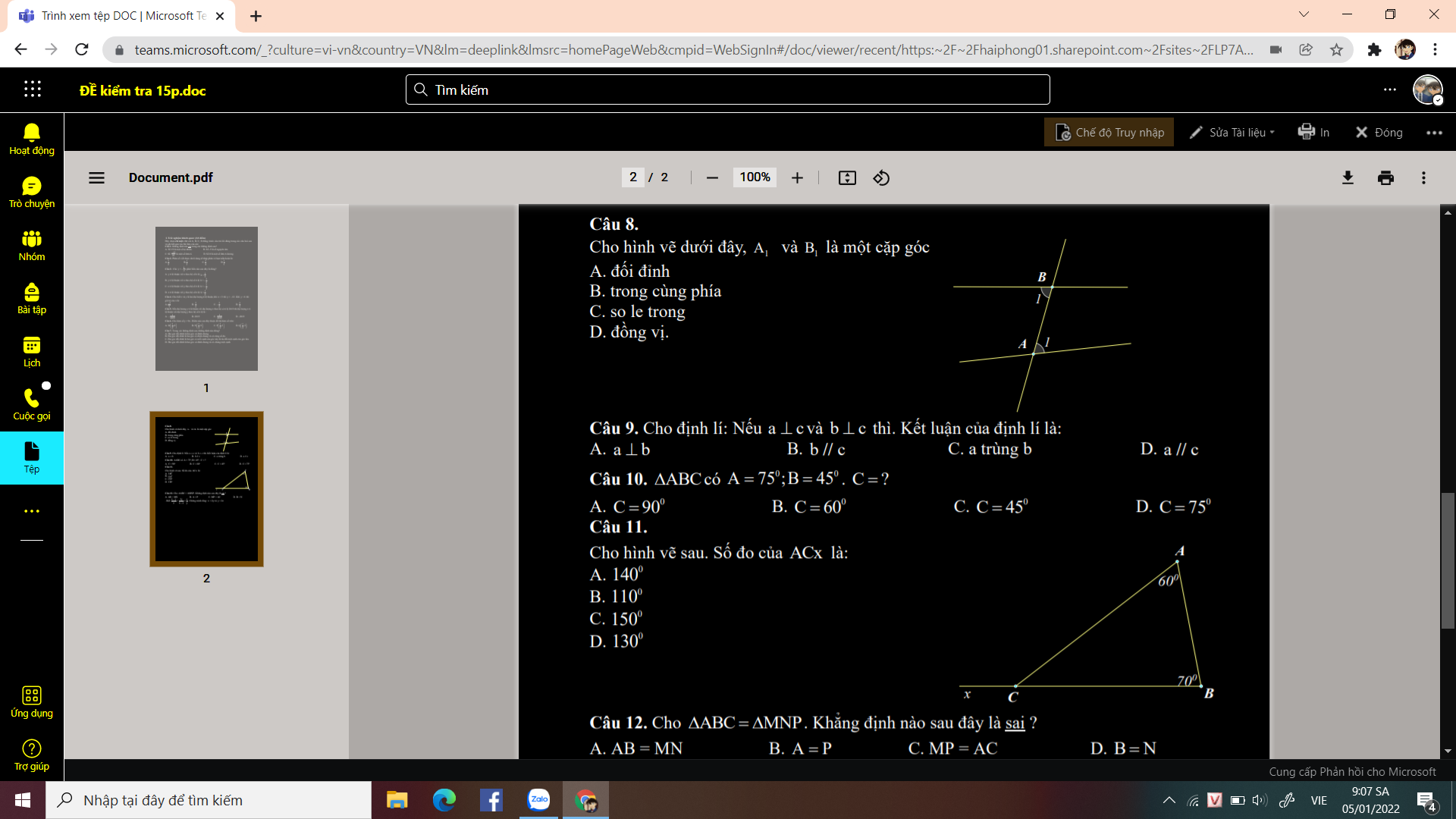




 GIÚP VỚI CẦN GẤP LẮM !!!
GIÚP VỚI CẦN GẤP LẮM !!! 


 Giúp mk vs ạ mk cần gấp . Cmơn mn nhé 😘
Giúp mk vs ạ mk cần gấp . Cmơn mn nhé 😘





 Các bn ơi , giúp mình bài này với , mik cần gấp lắm !!!!!!!!!!!!!!!!
Các bn ơi , giúp mình bài này với , mik cần gấp lắm !!!!!!!!!!!!!!!!
\(\text{8.C.So le trong}\)
\(\text{9.C.a trùng b}\)
\(\text{10.B.}60^0\)
\(\text{11.C.}150^0\)
\(\text{12.B.A=P}\)
thank bạn nha