
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) \(\sqrt{x^2}=\left|-8\right|\)
\(\Rightarrow\left|x\right|=8\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\)
d) \(\sqrt{9x^2}=\left|-12\right|\)
\(\Rightarrow\sqrt{\left(3x\right)^2}=12\)
\(\Rightarrow\left|3x\right|=12\)
\(\Rightarrow\left[{}\begin{matrix}3x=12\\3x=-12\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{12}{3}\\x=-\dfrac{12}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)

ĐKXĐ: \(\left\{{}\begin{matrix}2x-3>=0\\x+1>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\x>=-1\end{matrix}\right.\)
=>\(x>=\dfrac{3}{2}\)
\(\sqrt{2x-3}-\sqrt{x+1}=x-4\)
=>\(\dfrac{2x-3-x-1}{\sqrt{2x-3}+\sqrt{x+1}}-\left(x-4\right)=0\)
=>\(\left(x-4\right)\left(\dfrac{1}{\sqrt{2x-3}+\sqrt{x+1}}-1\right)=0\)
=>x-4=0
=>x=4(nhận)

Gọi số xe dự định tham gia chở hàng là x (xe) với x>4, x nguyên dương
Mỗi xe dự định chở khối lượng hàng là: \(\dfrac{20}{x}\) (tấn)
Số xe thực tế tham gia chở hàng là: \(x-4\) (xe)
Thực tế mỗi xe phải chở số hàng là: \(\dfrac{20}{x-4}\) (tấn)
Do thực tế mỗi xe phải chở nhiều hơn dự định là 5/6 tấn hàng nên ta có pt:
\(\dfrac{20}{x-4}-\dfrac{20}{x}=\dfrac{5}{6}\)
\(\Rightarrow24x-24\left(x-4\right)=x\left(x-4\right)\)
\(\Leftrightarrow x^2-4x-96=0\)
\(\Rightarrow\left[{}\begin{matrix}x=12\\x=-8\left(loại\right)\end{matrix}\right.\)
Vậy thực tế có \(12-4=8\) xe tham gia vận chuyển

Mình không thấy câu nào cả thì giúp kiểu gì lỗi ảnh hay sao ý

ĐKXĐ: \(x+2y\ne0\)
\(\left\{{}\begin{matrix}x-\dfrac{1}{x+2y}=\dfrac{7}{4}\\-\dfrac{5}{2}x+2+\dfrac{4}{x+2y}=-2\end{matrix}\right.\)
Đặt \(\dfrac{1}{x+2y}=z\) ta được hệ:
\(\left\{{}\begin{matrix}x-z=\dfrac{7}{4}\\-\dfrac{5}{2}x+4z=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\z=\dfrac{1}{4}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{x+2y}=\dfrac{1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\x+2y=4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

đây là bài lớp 10 chứ nhỉ
ta có \(AC=20\times2=40\text{ hải lí}\), \(AB=15\times2=30\text{ hải lí}\)
áp dụng định lý cosin ta có :
\(BC=\sqrt{AB^2+AC^2-2AB.AC\text{c}osA}=\sqrt{40^2+30^2-2\times30\times40\times cos60^o}\simeq36.06\text{ hải lí}\)

a, \(P=\frac{a^3-a+2b-\frac{b^2}{a}}{\left(1-\sqrt{\frac{a+b}{a^2}}\right)\left(a+\sqrt{a+b}\right)}:\left[\frac{a^2\left(a+b\right)+a\left(a+b\right)}{\left(a-b\right)\left(a+b\right)}+\frac{b}{a-b}\right]\)
\(=\frac{\frac{a^4-a^2-2ab-b^2}{a}}{\frac{\left(a-\sqrt{a+b}\right)\left(a+\sqrt{a+b}\right)}{a}}:\left[\frac{\left(a+b\right)\left(a^2+a\right)}{\left(a+b\right)\left(a-b\right)}+\frac{b}{a-b}\right]\)
\(=\frac{a^4-a^2-2ab-b^2}{a^2-a-b}:\frac{a^2+a+b}{a-b}\)
\(=\frac{a^4-a^2-2ab-b^2}{a^2-\left(a+b\right)}.\frac{a-b}{a^2+\left(a+b\right)}\)
\(=\frac{\left(a^4-a^2-2ab-b^2\right).\left(a-b\right)}{a^4-\left(a+b\right)^2}=\frac{\left[a^4-\left(a+b\right)^2\right].\left(a-b\right)}{a^4-\left(a+b\right)^2}=a-b\)
b, Có \(P=a-b=1\)\(\Rightarrow a=1+b\)
\(a^3-b^3=7\Leftrightarrow\left(a^2+ab+b^2\right)\left(a-b\right)=7\)
\(\Rightarrow a^2+ab+b^2=7\)
\(\Leftrightarrow\left(1+b\right)^2+\left(1+b\right)b+b^2=7\)
\(\Leftrightarrow b^2+2b+1+b^2+b+b^2=7\)
\(\Leftrightarrow3b^2+3b-6=0\)
Bạn tự giải phương trình tìm b => a
Bài 2 :
\(a,y=\left(m+1\right)x-2m-5\) \(\Leftrightarrow\left(m+1\right)x-2m-5-y=0\)
\(\Leftrightarrow mx+x-2m-5-y=0\)\(\Leftrightarrow m\left(x-2\right)+x-y-5=0\)
Có y luôn qua điểm A cố định với A( x0 ; y0 ) \(\orbr{\begin{cases}x_0-2=0\\x_0-y_0-5=0\end{cases}}\Rightarrow\orbr{\begin{cases}x_0=2\\y_0=-3\end{cases}}\)
=> A( 2;-3)
Gọi H là chân đường vuông góc hạ từ O xuống d => \(OH\le OA\)
\(OH_{max}=OA\)khi \(H\equiv A\)\(\left(d\perp OA\right)\)
=> đường thẳng OA qua O( 0;0 ) và A( 2;-3 ) => \(y=-\frac{3}{2}x\)
\(\Rightarrow d\perp OA\)=> hệ số góc \(m.\) \(-\frac{3}{2}=-1\Rightarrow m=\frac{2}{3}\)
b, \(y=0\Rightarrow\left(m+1\right)x-2m-5=0\)\(\Rightarrow x=\frac{2m+5}{m+1}\)\(\Rightarrow A\left(\frac{2m+5}{m+1};0\right)\)
\(x=0\Rightarrow y=-2m-5\Rightarrow B\left(0;-2m-5\right)\)
\(\Rightarrow OA=\sqrt{\frac{2m+5}{m+1}};OB=\sqrt{-2m-5}\)
\(\Rightarrow\frac{1}{2}.OA.OB=\frac{3}{2}\Rightarrow OA.OB=3\)
\(\Rightarrow\left(OA.OB\right)^2=9\Rightarrow\frac{\left(2m+5\right)^2}{m+1}=9\)
\(\Rightarrow4m^2+20m+25-9m-9=\)
\(\Rightarrow4m^2+11m+16=0\)

. . A B O H C D I
a) Vì AD là tiếp tuyến của (O)
=> \(AD\perp AB\)
=> \(\widehat{DAB}=90^o\)
CÓ: OA=OB=OC(=R)
=> CO là tiếp tuyến của ΔABC
Mà: \(CO=\frac{1}{1}AB\left(cmt\right)\)
=> ΔABC vuông tại C
=> \(AC\perp BC\)
Xét ΔABD vuông tại A(cmt), mà AC là đường cao(cmt)
=> \(BC\cdot BD=AB^2\) ( theo hệ thức trong tam giác vuông)
=> \(BC\cdot BD=\left(2\cdot OB\right)^2=4R^2\)
b) Có: OA=OC(cmt)
=> ΔOAC cân tại O
=> \(\widehat{ACO}=\widehat{CAO}\)
Xét ΔACD vuông tại C(cmt)
mà: CI là tiếp tuyến ứng vs cạnh AD
=> IC=IA
=> ΔIAC cân tại I
=> \(\widehat{IAC}=\widehat{ICA}\)
Có: \(\widehat{IAC}+\widehat{CAO}=\widehat{DAB}=90^o\)
=> \(\widehat{ICA}+\widehat{ACO}=90^o\)
Hay: \(\widehat{ICO}=90^o\)
=> IC là tiếp tuyến của (O)
Phần c đề sai

Bài 1:
Kẻ \(OM\perp AB\), \(OM\)cắt \(CD\)tại \(N\).
Khi đó \(MN=8cm\).
TH1: \(AB,CD\)nằm cùng phía đối với \(O\).
\(R^2=OC^2=ON^2+CN^2=h^2+\left(\frac{25}{2}\right)^2\)(\(h=CN\)) (1)
\(R^2=OA^2=OM^2+AM^2=\left(h+8\right)^2+\left(\frac{15}{2}\right)^2\)(2)
Từ (1) và (2) suy ra \(R=\frac{\sqrt{2581}}{4},h=\frac{9}{4}\).
TH2: \(AB,CD\)nằm khác phía với \(O\).
\(R^2=OC^2=ON^2+CN^2=h^2+\left(\frac{25}{2}\right)^2\)(\(h=CN\)) (3)
\(R^2=OA^2=OM^2+AM^2=\left(8-h\right)^2+\left(\frac{15}{2}\right)^2\)(4)
Từ (3) và (4) suy ra \(R=\frac{\sqrt{2581}}{4},h=\frac{-9}{4}\)(loại).
Bài 3:
Lấy \(A'\)đối xứng với \(A\)qua \(Ox\), khi đó \(A'\)có tọa độ là \(\left(1,-2\right)\).
\(MA+MB=MA'+MB\ge A'B\)
Dấu \(=\)xảy ra khi \(M\)là giao điểm của \(A'B\)với trục \(Ox\).
Suy ra \(M\left(\frac{5}{3},0\right)\).
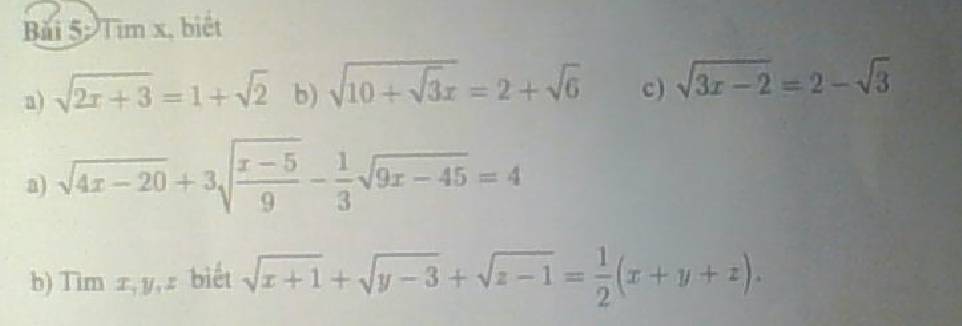



 Giải giúp mình với ạ, cần gấp lắm, cảm ơn
Giải giúp mình với ạ, cần gấp lắm, cảm ơn



5:
a: =>2x+3=3+2căn 2
=>2x=2căn 2
=>x=căn 2
b: =>10+căn 3x=10+4căn 6
=>căn 3x=4căn 6=căn 96
=>3x=96
=>x=32
c: =>3x-2=7-4căn 3
=>3x=9-4căn 3
=>x=3-4/3*căn 3
a: =>\(2\cdot\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\)
=>2*căn x-5=4
=>căn x-5=2
=>x-5=4
=>x=9