K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NL
1
6 tháng 12 2021
Bài 2:
Thay x=3 và y=-5 vào (d), ta được:
b-6=-5
hay b=1
1 tháng 12 2021
Hàm số bậc nhất \(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m=0\\2m^2+m\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\left(m-3\right)=0\\m\left(2m+1\right)\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=0\\m=3\end{matrix}\right.\\\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m=3\)
17 tháng 7 2019
Liên quan gì bạn @Tam Mai, chứng minh chứ không phải bấm máy tính
29 tháng 12 2021
2: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}=1\\\dfrac{1}{y}=\dfrac{4}{5}-\dfrac{1}{x}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{10}{3}\end{matrix}\right.\)
NP
1
9 tháng 7 2023
b: Gọi giao của AH với BC là F
=>AH vuông góc BC tại F
góic CHI=góc AHD=90 độ-góc HAD=góc ABC=1/2*sđ cung AC
góc CIH=1/2*sđ cung CA
=>góc CHI=góc CIH
=>ΔCHI cân tại C
c:
góc BDC=góc BEC=90 độ
=>BDEC nội tiếp đường tròn đường kính BC
=>MD=ME
=>ΔMDE cân tại M
mà MN là trung tuyến
nên MN vuông góc DE
Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC
=>góc xAC=góc AED
=>Ax//DE
=>DE vuông góc OA
=>MN//AO
1 tháng 7 2021
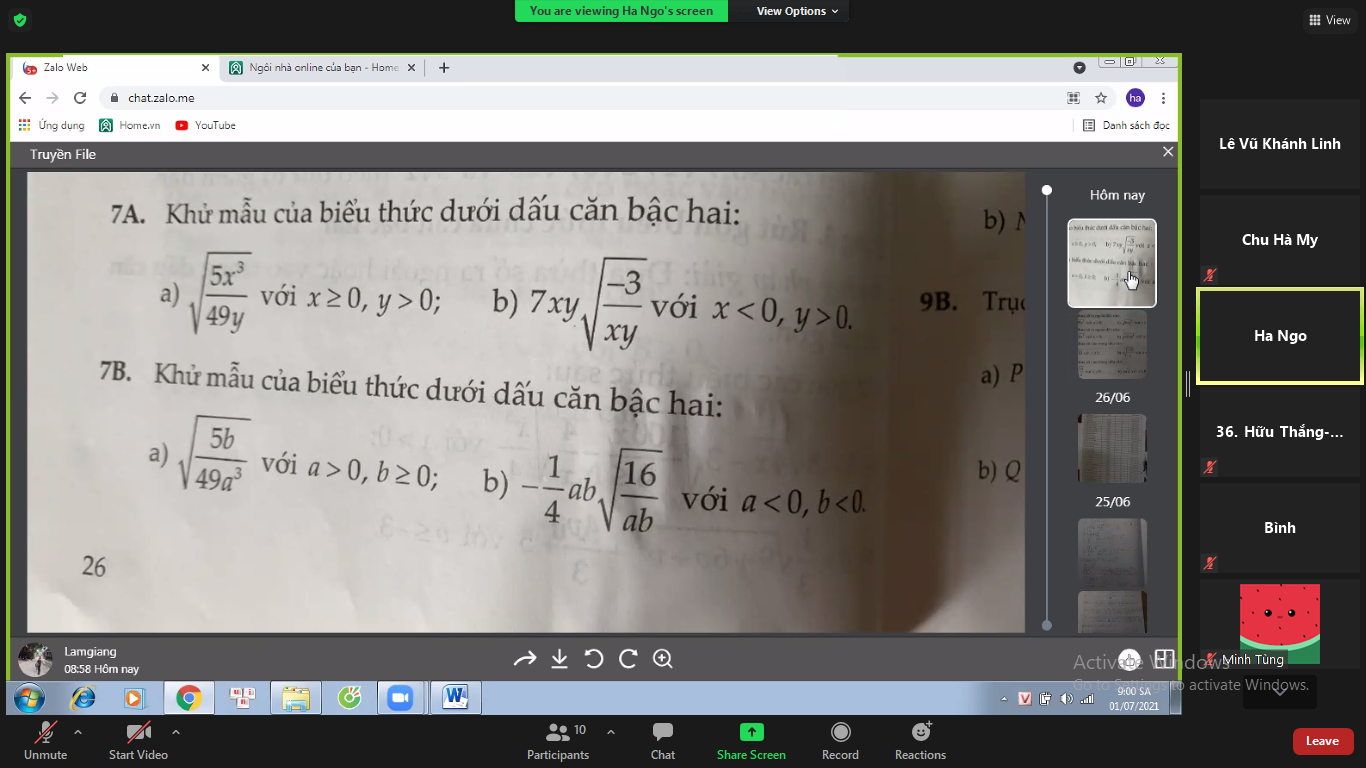
7A:
a) \(\sqrt{\dfrac{5x^3}{49y}}=\dfrac{\sqrt{5x^3}}{7\sqrt{y}}=\dfrac{\sqrt{5x^3y}}{7y}\)
b) \(7xy\sqrt{-\dfrac{3}{xy}}=7xy\cdot\dfrac{\sqrt{-3xy}}{xy}=7\sqrt{-3xy}\)
7B:
a) \(\sqrt{\dfrac{5b}{49a^3}}=\dfrac{\sqrt{5b}}{7a\sqrt{a}}=\dfrac{\sqrt{5ab}}{7a^2}\)
b) \(-\dfrac{1}{4}ab\sqrt{\dfrac{16}{ab}}=-\dfrac{1}{4}\cdot ab\cdot\dfrac{4\sqrt{ab}}{ab}=-\sqrt{ab}\)
