
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2x^2 + 0,82 = 1
2x^2 = 0,18
x^2 = 0,09
=> x = -0,3 hoặc 0,3
cho mik nha chế

Có phải bạn soạn nhầm 16 thành 6 đúng không :)
\(\frac{\frac{15}{8}-\frac{15}{16}-\frac{15}{32}+\frac{15}{64}}{3-\frac{3}{2}-\frac{3}{4}+\frac{3}{8}}\)
\(=\frac{15.\left(\frac{1}{2}-\frac{1}{4}-\frac{1}{8}+\frac{1}{16}\right)}{6.\left(\frac{1}{2}-\frac{1}{4}-\frac{1}{8}+\frac{1}{16}\right)}\)
\(=\frac{15}{6}\)
\(=\frac{5}{2}\)


Vì p nguyên tố > 5 nên p lẻ => p + 1 chẵn => p + 1 chia hết cho 2 (1)
Xét 3 số tự nhiên liên tiếp: p; p + 1; p + 2, trong 3 số này có 1 số chia hết cho 3
Do p và p + 2 nguyên tố > 5 nên 2 số này đều không chia hết cho 3
=> p + 1 chia hết cho 3 (2)
Từ (1) và (2), mà (2;3)=1 => p + 1 chia hết cho 6 (đpcm)

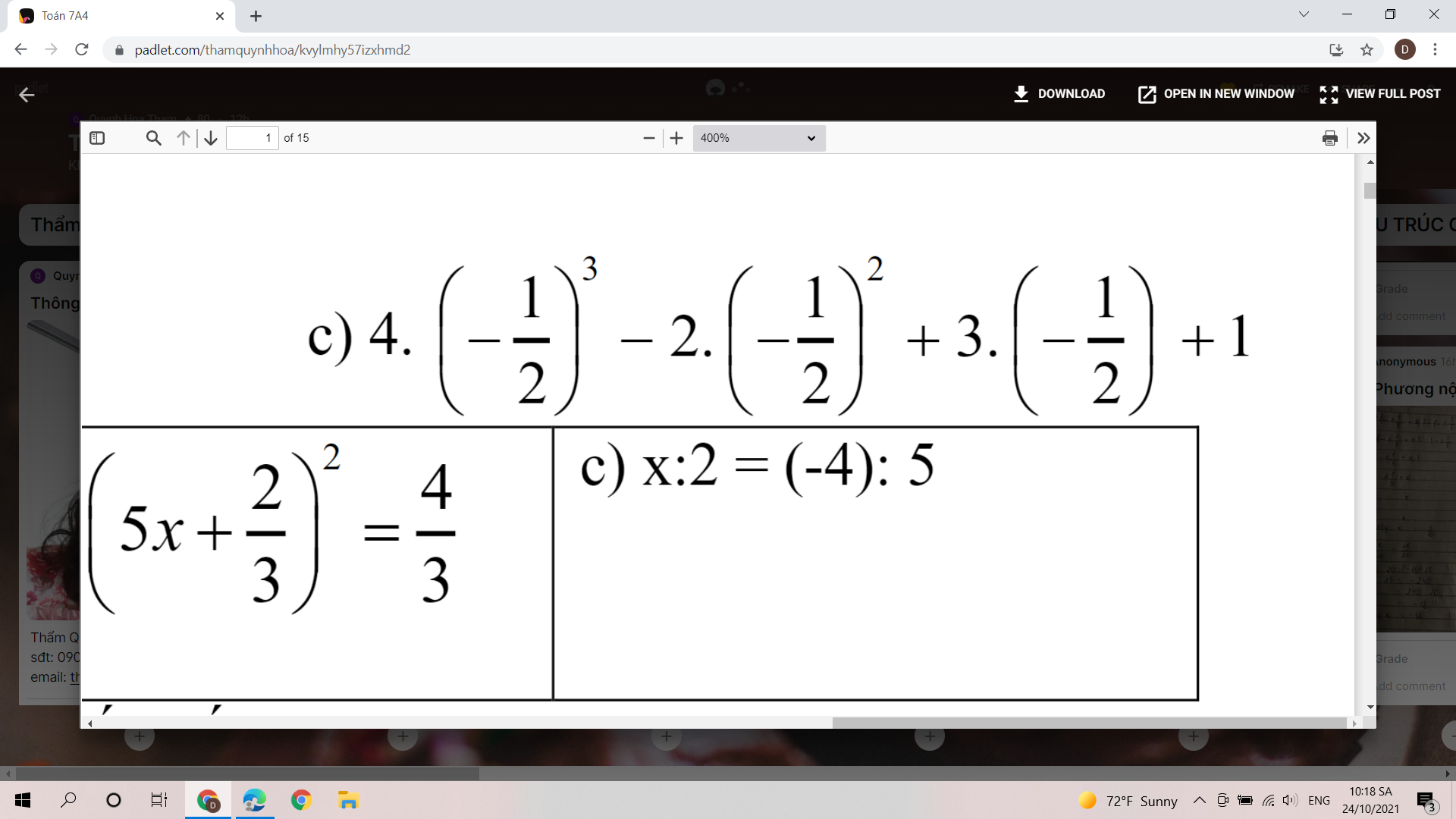
\(c,=4\cdot\left(-\dfrac{1}{8}\right)-2\cdot\dfrac{1}{4}-\dfrac{3}{2}+1=-\dfrac{1}{2}-\dfrac{1}{2}-\dfrac{3}{2}+1=-\dfrac{3}{2}\\ \left(5x+\dfrac{2}{3}\right)^2=\dfrac{1}{4}\Rightarrow\left[{}\begin{matrix}5x+\dfrac{2}{3}=\dfrac{1}{2}\\5x+\dfrac{2}{3}=-\dfrac{1}{2}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}5x=-\dfrac{1}{6}\\5x=-\dfrac{7}{6}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{30}\\x=-\dfrac{7}{30}\end{matrix}\right.\\ c,x:2=\left(-4\right):5\Rightarrow x=-\dfrac{4}{5}\cdot2=-\dfrac{8}{5}\)

a: Xét ΔABI và ΔAEI có
AB=AE
\(\widehat{BAI}=\widehat{EAI}\)
AI chung
Do đó: ΔABI=ΔAEI
b: Xét ΔABE có AB=AE
nên ΔABE cân tại A
mà AF là đường phân giác
nên AF là đường cao
c: \(\widehat{ABE}=\dfrac{180^0-80^0}{2}=50^0\)

a: Thay x=-2 vào A, ta được:
\(A=\dfrac{1}{4}\left(-2\right)^4+\dfrac{1}{2}\cdot\left(-2\right)^2-5\)
\(=\dfrac{1}{4}\cdot16+\dfrac{1}{2}\cdot4-5\)
=4+2-5
=1
b: \(A=\dfrac{1}{4}x^4+\dfrac{1}{2}x^2-5\)
\(=\left(\dfrac{1}{2}x^2\right)^2+2\cdot\dfrac{1}{2}x^2\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{21}{4}\)
\(=\left(\dfrac{1}{2}x^2+\dfrac{1}{2}\right)^2-\dfrac{21}{4}\)
ta có: \(\dfrac{1}{2}x^2>=0\forall x\)
=>\(\dfrac{1}{2}x^2+\dfrac{1}{2}>=\dfrac{1}{2}\forall x\)
=>\(\left(\dfrac{1}{2}x^2+\dfrac{1}{2}\right)^2>=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\forall x\)
=>\(A=\left(\dfrac{1}{2}x^2+\dfrac{1}{2}\right)^2-\dfrac{21}{4}>=\dfrac{1}{4}-\dfrac{21}{4}=-5\forall x\)
Dấu '=' xảy ra khi x=0

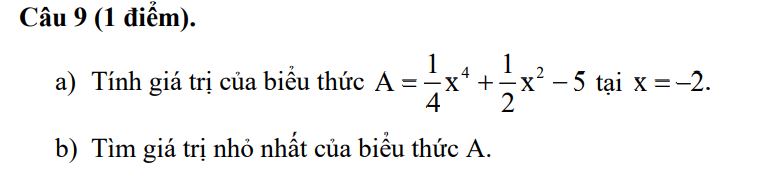
ta có :
\(\hept{\begin{cases}\left(x-\frac{2}{7}\right)^{2018}\ge0\\\left(0,2-\frac{1}{5}y\right)^{2020}\ge0\end{cases}}\)\(\Rightarrow P\ge2021\)
vậy GTNN của P =2021 khi \(\hept{\begin{cases}x=\frac{2}{7}\\y=1\end{cases}}\)
Thanks