
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1}{2!}+\frac{2}{3!}+\frac{3}{4!}+...+\frac{2014}{2015!}\)
\(=\frac{2}{2!}-\frac{1}{2!}+\frac{3}{3!}-\frac{1}{3!}+\frac{4}{4!}-\frac{1}{4!}+...+\frac{2015}{2015!}-\frac{1}{2015!}\)
\(=1-\frac{1}{2!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{3!}-\frac{1}{4!}+...+\frac{1}{2014!}-\frac{1}{2015!}\)
\(=1-\frac{1}{2015!}< 1\left(đpcm\right)\)

a/ Theo bài ra: \(x^2+y^2=6;xy=1\)
=> \(x^2+y^2+2xy=8\)
=> \(\left(x+y\right)^2=8\)
=> \(x+y=\sqrt{8}\)
b/ Theo bài ra: \(x^2+y^2=14;xy=1\)
=>\(x^2+y^2-2xy=12\)
=> \(\left(x-y\right)^2=12\)
=> \(x-y=\sqrt{12}\)
c/ Theo bài ra: \(a^2+b^2=116;ab=40\)
=> \(\left(a^2+b^2\right)^2=116^2;a^2b^2=1600\)
=> \(a^4+b^4+2a^2b^2=116^2\)
=> \(a^4-2a^2b^2+b^4+4a^2b^2=13456\)
=> \(a^4-2a^2b^2+b^4=7056\)


đề 1 bài 4
xét tam gics ABC và tam giác HBA có
góc B chung
góc BAC = góc BHA (=90 độ)
=> tam giác ABC đồng dạng vs tam giác HBA (g.g)
=> AB/HB=BC/AB=> AB^2=HB *BC
áp dụng đl py ta go trog tam giác vuông ABC có
BC^2 = AB^2 +AC^2=6^2+8^2=100
=> BC =\(\sqrt{100}\)=10 cm
ta có tam giác ABC đồng dạng vs tam giác HBA (cm câu a )
=> AC/AH=BC/BA=>AH=8*6/10=4.8CM
=>AB/BH=AC/AH=> BH=6*4.8/8=3,6cm
=>HC =BC-BH=10-3,6=6,4cm
dề 1 bài 1
5x+12=3x -14
<=>5x-3x=-14-12
<=>2x=-26
<=> x=-12
vạy S={-12}
(4x-2)*(3x+4)=0
<=>4x-2=0<=>x=1/2
<=>3x+4=0<=>x=-4/3
vậy S={1/2;-4/3}
đkxđ : x\(\ne2;x\ne-3\)
\(\dfrac{4}{x-2}+\dfrac{1}{x+3}=0\)
<=> 4(x+3)/(x-2)(x+3)+1(x-2)/(x-2)(x+3)
=> 4x+12+x-2=0
<=>5x=-10
<=>x=-2 (nhận)
vậy S={-2}

Bài 2 nhìn tổng quát thì tahays tiwur A đến K đều dung hđt số 3
còn L thì đặt dyas âm trước 3 hạng tử đầu dung hđt 1 rồi áp dụng hđt 3
m tương tự đặt dấu âm làm nhân tử chung 3 hạng tử sau rồi áp dụng hđt số 2 sung hđt số 3
.hết

Câu 6: Tìm giá trị nhỏ nhất của biểu thức : \(A=x^2-2x+2\)
\(A=x^2-2x+2\)
\(A=\left(x^2-2.x.1+1^2\right)+2\)
\(A=\left(x-1\right)^2+2\)
Nhận xét : \(\left(x-1\right)^2\ge0\) với mọi x
\(\Rightarrow\left(x-1\right)^2+2\ge2\) với mọi x
\(\Rightarrow A\ge2\)
Vậy biểu thức A bằng 2 đạt được khi :
\(\left(x-1\right)^2=0\)
\(x-1=0\)
\(x=1\)

uk đi đi cho đỡ tốn diện tích khi Nam đăg câu hỏi câu trả lời của Nam
 giup minh voi bai 4 nha
giup minh voi bai 4 nha moi nguoi giup minh bai nay nha
moi nguoi giup minh bai nay nha
 giup minh voi
giup minh voi giup minh voi
giup minh voi









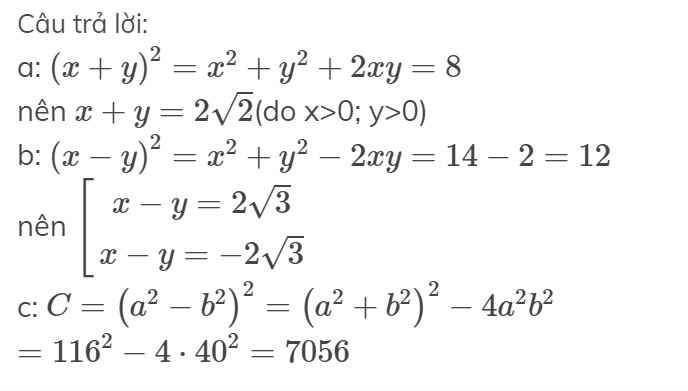


 l
l ại làm phiền nhau rồi giúp mk nha các ty
ại làm phiền nhau rồi giúp mk nha các ty




