
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\dfrac{x-1}{x+5}=\dfrac{6}{7}\left(đk:x\ne-5\right)\)
\(\Rightarrow7\left(x-1\right)=6\left(x+5\right)\)
\(\Rightarrow x=37\left(tm\right)\)
b) \(\dfrac{x^2}{6}=\dfrac{24}{49}\)
\(\Rightarrow x^2=\dfrac{24.6}{49}=\dfrac{144}{49}\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{12}{7}\\x=-\dfrac{12}{7}\end{matrix}\right.\)

a) Xét \(\Delta ADE\) và \(\Delta ABC:\)
\(AD=AB\left(gt\right).\\ AE=AC\left(gt\right).\)
\(\widehat{DAE}=\widehat{BAC}\) (2 góc đối đỉnh).
\(\Rightarrow\Delta ADE=\Delta ABC\left(c-g-c\right).\)
b) Ta có: \(\widehat{OBE}=180^o-\widehat{ABC};\widehat{ODC}=180^o-\widehat{ADE}.\)
Mà \(\widehat{ABC}=\widehat{ADE}\left(\Delta ABC=\Delta ADE\right).\)
\(\Rightarrow\widehat{OBE}=\widehat{ODC}.\)
Ta có: \(BE=BA+AE;DC=DA+AC.\)
Mà \(BA=DA;AE=AC\left(gt\right).\)
\(\Rightarrow BE=DC.\)
Xét \(\Delta OBE\) và \(\Delta ODC:\)
\(\widehat{OBE}=\widehat{ODC}\left(cmt\right).\\ BE=DC\left(cmt\right).\\ \widehat{BEO}=\widehat{DCO}\left(\Delta ADE=\Delta ABC\right).\\ \Rightarrow\Delta OBE=\Delta ODC\left(g-c-g\right).\)
c) \(\Delta OBE=\Delta ODC\left(cmt\right).\)
\(\Rightarrow OB=OD\) (2 cạnh tương ứng).
d) Xét \(\Delta OAE\) và \(\Delta OAC:\)
\(OAchung.\\ OE=OC\left(\Delta OBE=\Delta ODC\right).\\ AE=AC\left(gt\right).\\ \Rightarrow\Delta OAE=\Delta OAC\left(c-c-c\right).\)
\(\Rightarrow\widehat{AOE}=\widehat{AOC}\) (2 góc tương ứng).
\(\Rightarrow OA\) là tia phân giác của \(\widehat{COE}.\)

a: \(2^{300}=8^{100}\)
\(3^{200}=9^{100}\)
mà 8<9
nên \(2^{300}< 3^{200}\)

\(A=\dfrac{2^{10}\cdot3^8}{2^{10}\cdot3^8\cdot2^8\cdot3^8\cdot2^2\cdot5}+\dfrac{2^{12}\cdot3^{10}+2^3\cdot3\cdot5\cdot2^9\cdot3^9}{2^{16}\cdot3^{12}+2^{18}\cdot3^{18}}\\ A=\dfrac{1}{2^{10}\cdot3^8\cdot5}+\dfrac{2^{12}\cdot3^{10}\left(1+5\right)}{2^{16}\cdot3^{12}\left(1+2^2\cdot3^6\right)}\\ A=\dfrac{1}{2^{10}\cdot3^8\cdot5}+\dfrac{6}{2^4\cdot3^2\cdot2917}=\dfrac{1}{2^{10}\cdot3^8\cdot5}+\dfrac{1}{2^3\cdot3\cdot2917}\)


\(\dfrac{7-y}{3}=\dfrac{6-2y}{2}\)
\(\Rightarrow3\left(6-2y\right)=2\left(7-y\right)\)
\(\Rightarrow18-6y=14-2y\Rightarrow4y=4\Rightarrow y=1\)


Tên tam giác là MNP
Tên 3 đỉnh là M,N,P
Tên 3 góc là \(\widehat{mNp};\widehat{nMp};\widehat{nPm}\)
Tên 3 cạnh là MN, NP, MP

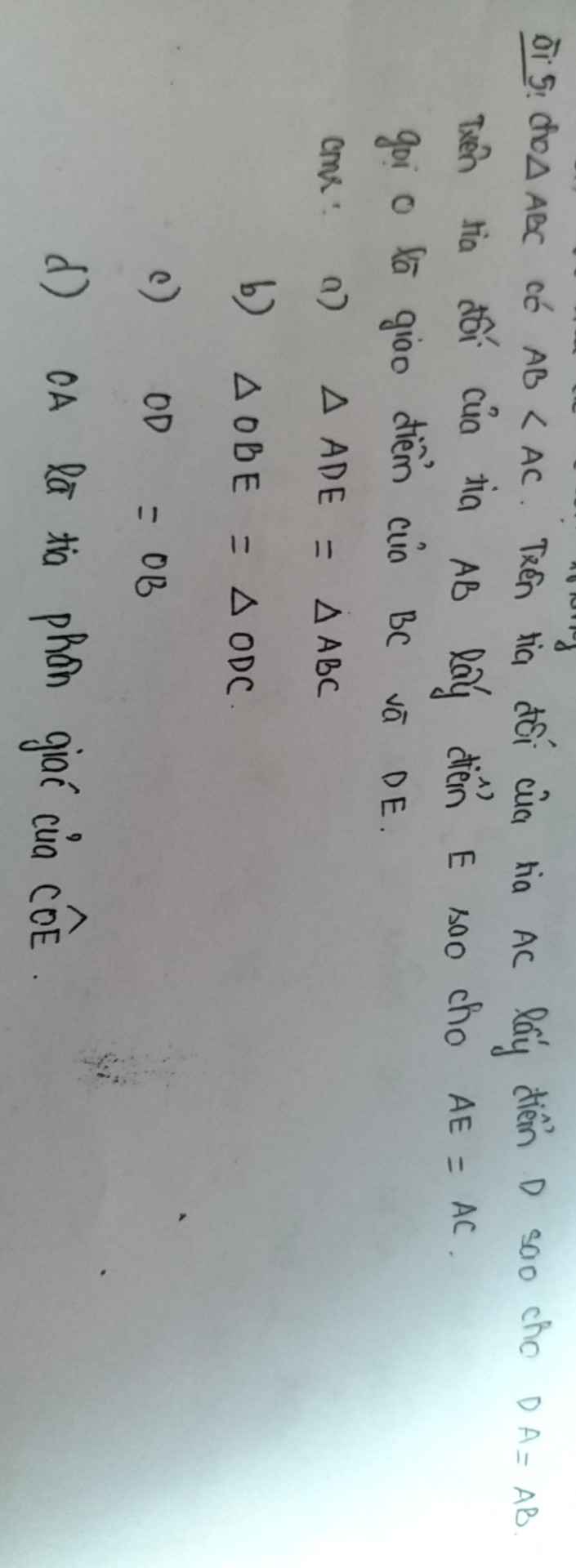

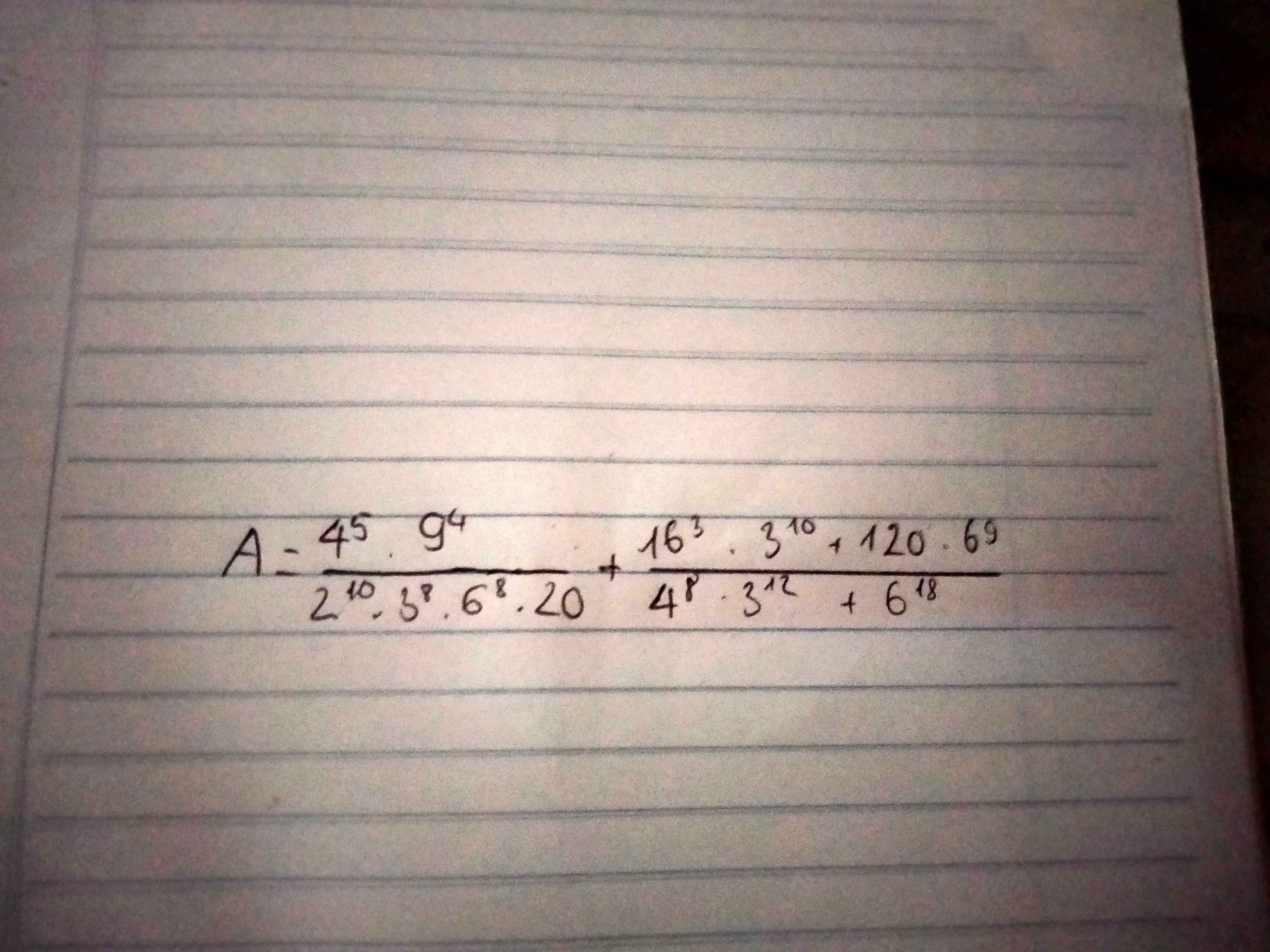

 giúp mình với, mk đang cần gấp ạ ! thanks mn rất nhiều ạ
giúp mình với, mk đang cần gấp ạ ! thanks mn rất nhiều ạ