Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) bn lm đc rồi nên mk bỏ qua nhé
b) Áp dụng định lý Putago vào tam giác vuông ABC ta có
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=21^2+28^2=1225\)
\(\Leftrightarrow\)\(BC=\sqrt{1225}=35\)cm
\(\Delta ABC\)vuông tại \(A\)có \(AM\)là trung tuyến
\(\Rightarrow\)\(AM=\frac{1}{2}BC=17,5\)cm
\(\Delta HBA~\Delta ABC\) (câu a)
\(\Rightarrow\)\(\frac{AH}{AC}=\frac{AB}{BC}\)
\(\Rightarrow\)\(AH=\frac{AB.AC}{BC}=\frac{21.28}{35}=16,8\)cm
c) \(\Delta BAC\)có \(EM\)\(//\)\(AC\) (cùng vuông góc với AB)
\(\Rightarrow\)\(\frac{AE}{AB}=\frac{CM}{CB}\) (1)
\(\Delta CAB\) có \(MF\)\(//\)\(AB\) (cùng vuông góc với AC)
\(\Rightarrow\) \(\frac{AF}{AC}=\frac{BM}{BC}\) (2)
\(\Delta ABC\)có \(AM\)là trung tuyến
\(\Rightarrow\)\(MB=MC\)(3)
Từ (1), (2) và (3) suy ra:
\(\frac{AE}{AB}=\frac{AF}{AC}\)
\(\Rightarrow\)\(EF\)\(//\)\(BC\) (định lý Ta-lét đảo)

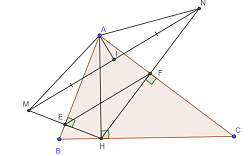
Đoạn thẳng f: Đoạn thẳng [A, B] Đoạn thẳng g: Đoạn thẳng [B, C] Đoạn thẳng h: Đoạn thẳng [A, C] Đoạn thẳng j: Đoạn thẳng [A, H] Đoạn thẳng k: Đoạn thẳng [H, M] Đoạn thẳng l: Đoạn thẳng [N, H] Đoạn thẳng m: Đoạn thẳng [M, N] Đoạn thẳng n: Đoạn thẳng [A, N] Đoạn thẳng p: Đoạn thẳng [A, M] Đoạn thẳng q: Đoạn thẳng [E, F] Đoạn thẳng r: Đoạn thẳng [A, I] Đoạn thẳng t: Đoạn thẳng [I, D] A = (9.91, 10.29) A = (9.91, 10.29) A = (9.91, 10.29) B = (3.97, -8.27) B = (3.97, -8.27) B = (3.97, -8.27) C = (33.4, -8.47) C = (33.4, -8.47) C = (33.4, -8.47) Điểm H: Giao điểm đường của i, g Điểm H: Giao điểm đường của i, g Điểm H: Giao điểm đường của i, g Điểm M: H đối xứng qua f Điểm M: H đối xứng qua f Điểm M: H đối xứng qua f Điểm N: H đối xứng qua h Điểm N: H đối xứng qua h Điểm N: H đối xứng qua h Điểm E: Giao điểm đường của f, k Điểm E: Giao điểm đường của f, k Điểm E: Giao điểm đường của f, k Điểm F: Giao điểm đường của h, l Điểm F: Giao điểm đường của h, l Điểm F: Giao điểm đường của h, l Điểm I: Trung điểm của m Điểm I: Trung điểm của m Điểm I: Trung điểm của m Điểm D: Giao điểm đường của s, q Điểm D: Giao điểm đường của s, q
a) Do EM = EH và AE vuông góc MH tại E nên AB là đường trung trực của MH. Tương tự AC là trung trực HN.
b) Do AB là đường trung trực của MH nên AM = AH. Tương tự AH = AN
Vậy AM = AN hay tam giác AMN cân tại A.
c) Xét tam giác HMN có E, F lần lượt là trung điểm HM, HN nên EF là đường trung bình tam giác.
Vậy EF // MN.
d) Tam giác cân AMN có I là trung điểm MN nên \(AI⊥MN\)
Lại có MN //EF nên \(AI⊥EF.\)

a) Ta thấy AB vuông góc với MH tại trung điểm E của MH nên AB là đường trung trực của MH.
Ta thấy AC vuông góc với NH tại trung điểm F của NH nên AC là đường trung trực của NH.
b) Do AB là trung trực của MH nên AM = AH.
Tương tự AN = AH. Vậy nên AM = AN hay tam giác AMN cân tại A.
c) Xét tam giác HMN có E là trung điểm MH, F là trung điểm HN nên EF là đường trung bình tam giác HMN.
Suy ra EF // MN.
d) Do tam giác AMN cân tại A nên trung tuyến AI đồng thời là đường cao. Vậy AI vuông góc MN.
Lại có MN // EF nên AI vuông góc EF.

A B C H E F M N
Theo tính chất đường thẳng song song :
\(AK=KI=IH\)( gt )
=> AE = EM = MB
=> AF = FN = NC
Theo bài ra ta có : \(\frac{MN}{BC}=\frac{AM}{MB}=\frac{2MB}{MB}=2\)cm
\(\frac{EF}{BC}=\frac{AE}{EB}=\frac{AE}{2AE}=\frac{1}{2}\)cm
hay \(2EF=BC\)(*)
Ta có : \(S_{ABC}=\frac{1}{2}AH.BC=90\)( gt )
\(\Delta AMN\)có EF là đường trung bình ( AE = EM ; AF = FN )
Suy ra : EF // MN và EF = 1/2 MN
Ta có : \(S_{MNEF}=\frac{\left(EF+MN\right).IK}{2}\)mà \(IK=\frac{1}{3}AH\)
\(=\frac{\left(EF+MN\right).\frac{AH}{3}}{2}=\frac{\left(EF+2EF\right).\frac{AH}{3}}{2}\)
\(=\frac{EF.AH}{2}\)mà \(2EF=BC\)cmt (*)
\(=\frac{\frac{BC}{2}.AH}{2}=\frac{BC.AH}{4}\)
Vậy \(S_{MNEF}=\frac{180}{4}=45\)cm2