K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
mình đang cần gấp, gải nhanh giúp mình với ạ!!!!!
16 tháng 6 2023
9:
a: BC^2=AB^2+AC^2
=>ΔABC vuông tại A
b: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>DA=DE và BA=BE
c: DA=DE
DA<DF
=>DE<DF
11 tháng 8 2023
\(=\dfrac{3}{2}-\dfrac{2}{21}-\dfrac{7}{12}+\left[\dfrac{15}{21}-\dfrac{1}{3}+\dfrac{5}{4}-\dfrac{2}{7}-\dfrac{1}{3}\right]\)
=11/12-2/21+5/7-2/3+5/4-2/7
=11/12-2/3+5/4-2/21+3/7
=11/12-8/12+15/12-2/21+9/21
=18/12+7/21
=3/2+1/3
=9/6+2/6=11/6
NA
Nguyễn An Ninh
VIP
14 tháng 8 2023
\(B=\dfrac{3}{2}-\dfrac{2}{21}-\left\{\dfrac{7}{12}-\left[\dfrac{15}{21}-\left(\dfrac{1}{3}-\dfrac{5}{4}\right)-\left(\dfrac{2}{7}+\dfrac{1}{3}\right)\right]\right\}\)
\(B=\dfrac{3}{2}-\dfrac{2}{21}-\left\{\dfrac{7}{12}-\left[\dfrac{15}{21}-\left(-\dfrac{11}{12}\right)-\dfrac{13}{21}\right]\right\}\)
\(B=\dfrac{3}{2}-\dfrac{2}{21}-\left\{\dfrac{7}{12}-\dfrac{85}{84}\right\}\)
\(B=\dfrac{3}{2}-\dfrac{2}{21}-\left(-\dfrac{3}{7}\right)\)
\(B=\dfrac{11}{6}\)
NL
0
MH
16 tháng 9 2021
1) \(\left(\dfrac{-13}{17}-\dfrac{31}{52}\right)-\left(\dfrac{73}{52}-\dfrac{13}{17}+\dfrac{5}{6}\right)-\dfrac{3}{4}\)
\(=\dfrac{-13}{17}-\dfrac{31}{52}-\dfrac{73}{52}+\dfrac{13}{17}-\dfrac{5}{6}-\dfrac{3}{4}\)
\(=\left(\dfrac{-13}{17}+\dfrac{13}{17}\right)-\left(\dfrac{31}{52}+\dfrac{73}{52}\right)-\left(\dfrac{5}{6}+\dfrac{3}{4}\right)\)
\(=0-2-\dfrac{19}{12}\)
\(=-2-\dfrac{19}{12}\)
\(=\dfrac{-43}{12}\)
NN
Giúp mình với ạ mình đang cần gấp:((
2
29 tháng 12 2021
a) \(4\sqrt{x}=8\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\)
b) \(\left(x-1\right)^2=9\Leftrightarrow x-1=3\Leftrightarrow x=4\)
29 tháng 12 2021
c: Áp dung tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{9}=\dfrac{x+y}{4+9}=3\)
Do đó: x=12; y=27
H9
HT.Phong (9A5)
CTVHS
5 tháng 7 2023
Bài 5:
a) \(x:\left(-\dfrac{1}{2}\right)^3=-\dfrac{1}{2}\)
\(\Rightarrow x=\left(-\dfrac{1}{2}\right)^3\cdot\left(-\dfrac{1}{2}\right)\)
\(\Rightarrow x=\left(\dfrac{1}{2}\right)^4=\dfrac{1}{16}\)
b) \(\left(\dfrac{3}{4}\right)^5\cdot x=\left(\dfrac{3}{4}\right)^7\)
\(\Rightarrow x=\left(\dfrac{3}{4}\right)^7:\left(\dfrac{3}{4}\right)^5\)
\(\Rightarrow x=\left(\dfrac{3}{4}\right)^2=\dfrac{9}{16}\)
c) \(\left(\dfrac{2}{3}\right)^5:x=\left(\dfrac{2}{3}\right)^3\)
\(\Rightarrow x=\left(\dfrac{2}{5}\right)^5:\left(\dfrac{2}{3}\right)^3\)
\(\Rightarrow x=\left(\dfrac{2}{5}\right)^2=\dfrac{4}{25}\)
d) \(\dfrac{25}{5^x}=5\)
\(\Rightarrow5^x\cdot5=25\)
\(\Rightarrow5^{x+1}=25\)
\(\Rightarrow5^{x+1}=5^2\)
\(\Rightarrow x+1=2\)
\(\Rightarrow x=2-1=1\)
e) \(\left(-\dfrac{1}{3}\right)^{x-5}=\dfrac{1}{81}\)
\(\Rightarrow\left(-\dfrac{1}{3}\right)^{x-5}=\left(-\dfrac{1}{3}\right)^4\)
\(\Rightarrow x-5=4\)
\(\Rightarrow x=4+5=9\)
g) \(\left(2x-3\right)^2=9\)
\(\Rightarrow\left(2x-3\right)=3^2\)
\(\Rightarrow2x-3=3\)
\(\Rightarrow2x=6\)
\(\Rightarrow x=\dfrac{6}{2}=3\)
h) \(\left(x+5\right)^3=64\)
\(\Rightarrow\left(x+5\right)^3=4^3\)
\(\Rightarrow x+5=4\)
\(\Rightarrow x=4-5=-1\)
i) \(2^{3x+2}=4^{x+5}\)
\(\Rightarrow2^{3x+2}=\left(2^2\right)^{x+5}\)
\(\Rightarrow2^{3x+2}=2^{2x+10}\)
\(\Rightarrow3x+2=2x+10\)
\(\Rightarrow3x-2x=10-2\)
\(\Rightarrow x=8\)
k) \(5^{x+1}-5^x=500\)
\(\Rightarrow\left(5-1\right)\cdot5^x=500\)
\(\Rightarrow4\cdot5^x=500\)
\(\Rightarrow5^x=125\)
\(\Rightarrow5^x=5^3\)
\(\Rightarrow x=3\)
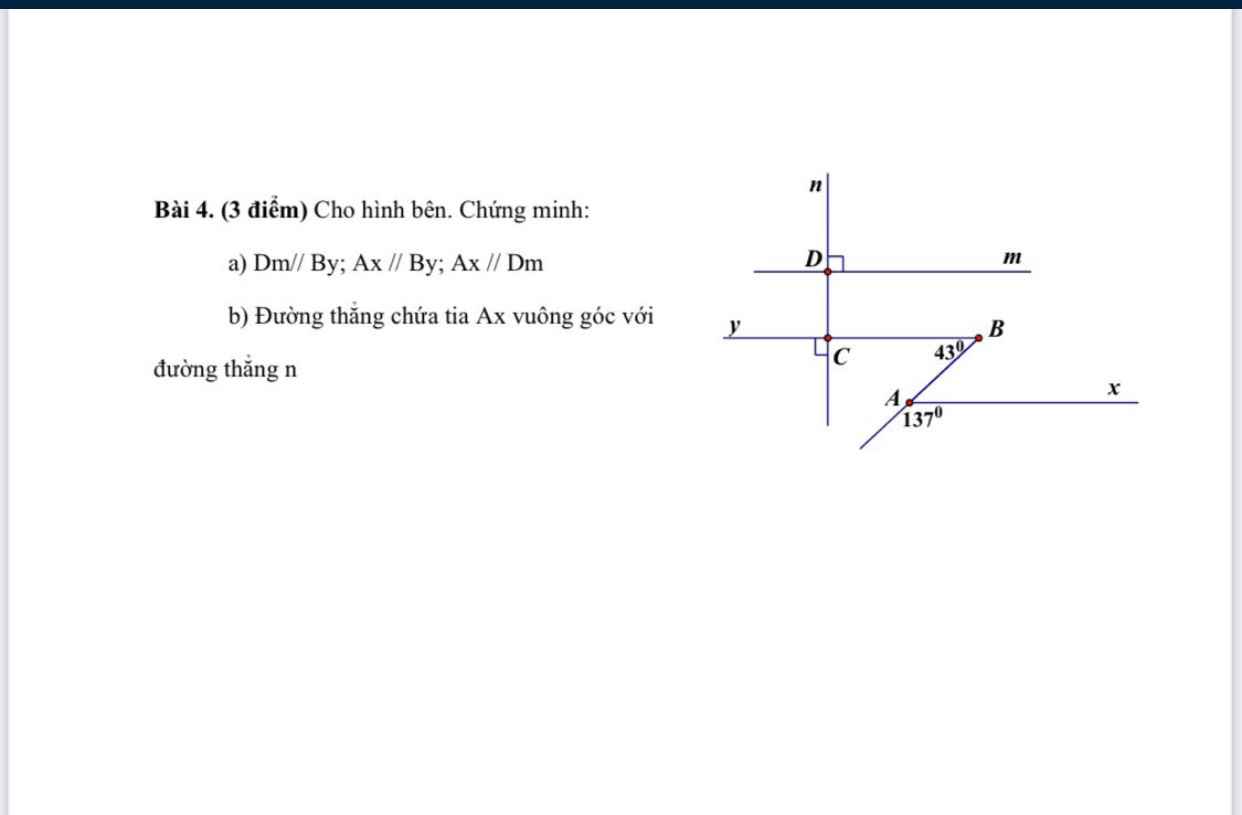
Bạn dùng so le trong, đồng vị và đối đỉnh đấy