K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
13 tháng 10 2021
1. Chọn B.
2. Chọn B.
3. Chọn D.
4. Chọn B.
5. Chọn D.
6. Chọn A.
7. Chọn D.
8. Chọn A.
9. Chọn D.
10. Chọn C.
11. Chọn A.
12.Chọn B.
SC
12 tháng 1 2022
Tuyệt vời, đợi mình load rồi mình hỏi thêm vào câu nữa nha bẹn
LN
1
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 9 2021
a.
\(y'=4x^3-4x=4x\left(x^2-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
Dấu y' trên trục số:
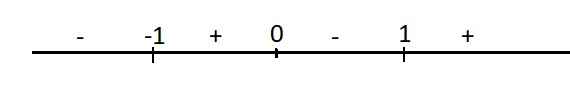
Hàm đồng biến trên các khoảng \(\left(-1;0\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
b.
\(y'=x^2+6x-7=0\Rightarrow\left[{}\begin{matrix}x=-7\\x=1\\\end{matrix}\right.\)
Dấu của y' trên trục số:
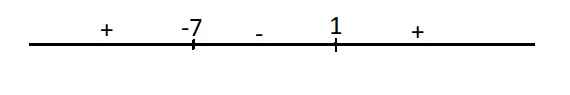
Hàm đồng biến trên các khoảng \(\left(-\infty;-7\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-7;1\right)\)
11 tháng 8 2016
kẻ CE//BD ( E thuộc AD)
=> d( BD;SC)= d( BD; ( SCE))=d( O; ( SCE))
kẻ OK _|_SC
OC_|_ CE
SO_|_CE => CE_|_ ( SOC) => CE_|_OK
do đó OK_|_(SCE)=> d(O;(SCE))=OK
1/OK^2=1/SO^2+1/OC^2
11 tháng 8 2016
câu 2:
BC//AD=> d( BC;SA)=d(BC:(SAD))=d( B;( SAD))=2 d( O; (SAD))
kẻ OH_|_ AD
kẻ OE_|_SH
ta có OH_|_AD; SO_|_AD=> AD_|_(SOH)=> AD_|_ OE
do đó OE_|_( SAD)=> d( O; (SAD))=OE
TP
11 tháng 7 2016
Một đường thẳng muốn vuông góc với một mặt phẳng thì phải vuông góc với 2 đường thẳng chéo nhau chứ bạn? ở ba câu trên bạn mới chứng minh nó vuông với 1 đường mà
HT
10 tháng 4 2021
31/
\(3z^2-2z+27=0\)
\(\Delta'=\left(-1\right)^2-3.27=1-3.27=-80\)
\(\Delta'\) có 2 căn bậc 2 là \(\pm4i\sqrt{5}\)
\(\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1+4i\sqrt{5}}{3}\\z_2=\dfrac{1-4i\sqrt{5}}{3}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\left(\dfrac{1}{3}\right)^2+\left(\dfrac{4\sqrt{5}}{3}\right)^2}=3\)
\(\Rightarrow z_1\left|z_2\right|+z_2\left|z_1\right|=1+4i\sqrt{5}+1-4i\sqrt{5}=2\) => A
32/ \(\Delta'=4-29=-25\Rightarrow\left\{{}\begin{matrix}z_1=-2+5i\\z_2=-2-5i\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{2^2+5^2}=\sqrt{29}\)
\(\Rightarrow\left|z_1\right|^4+\left|z_2\right|^4=2.\sqrt{29^4}=1682\) => B
33/ \(\Delta=1-12=-11\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1+i\sqrt{11}}{6}\\z_2=\dfrac{1-i\sqrt{11}}{6}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\left(\dfrac{1}{6}\right)^2+\left(\dfrac{\sqrt{11}}{6}\right)^2}=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\left|z_1\right|+\left|z_2\right|=\dfrac{2\sqrt{3}}{3}\) => D
34/ \(\Delta=1-4.3.2=-23\Rightarrow\left\{{}\begin{matrix}z_1=\dfrac{1-i\sqrt{23}}{6}\\z_2=\dfrac{1+i\sqrt{23}}{6}\end{matrix}\right.\Rightarrow\left|z_1\right|=\left|z_2\right|=\sqrt{\dfrac{1}{36}+\dfrac{23}{36}}=\dfrac{\sqrt{6}}{3}\)
\(\Rightarrow T=2.\left(\dfrac{\sqrt{6}}{3}\right)^2=\dfrac{4}{3}\) => C