
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


câu 2 phần 2:
\(\left\{{}\begin{matrix}4x+3y=11\\4x-y=7\end{matrix}\right.\)\(< =>\left\{{}\begin{matrix}4y=4\\4x-y=7\end{matrix}\right.< =>\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\).Vậy hệ pt có nghiệm
(x,y)=(2;1)
caau3 phần 2:
\(x^2-2x+m-1=0\)(1)
\(\Delta'=\left(-1\right)^2-\left(m-1\right)=1-m+1=2-m\)
để pt (1) có 2 nghiệm x1,x2<=>\(\Delta'\ge0< =>2-m\ge0< =>m\le2\)
theo vi ét=>\(\left\{{}\begin{matrix}x1+x2=2\left(1\right)\\x1.x2=m-1\left(3\right)\end{matrix}\right.\)
có: \(x1^4\)\(-x1^3=x2^4-x2^3\)
\(< =>x1^4-x2^4-x1^3+x2^3=0\)
\(< =>\left(x1^2-x2^2\right)\left(x1^2+x2^2\right)-\left(x1^3-x2^3\right)\)\(=0\)
\(< =>\left(x1-x2\right)\left(x1+x2\right)\left[\left(x1+x2\right)^2-2x1x2\right]\)\(-\left(x1-x2\right)\left(x1^2+x1x2+x^2\right)=0\)
\(< =>\)\(\left(x1-x2\right)\left[2.2^2-2\left(m-1\right)-\left(x1^2+x1x2+x2^2\right)\right]=0\)
\(< =>.\left(x1-x2\right)\left[8-2m+2-\left(x1+x2\right)^2+x1x2\right]=0\)
<=>\(\left(x1-x2\right)\left[10-2m-4+m-1\right]=0\)
\(< =>\left(x1-x2\right)\left(5-m\right)=0\)
\(=>\left[{}\begin{matrix}x1-x2=0\\5-m=0\end{matrix}\right.< =>\left[{}\begin{matrix}x1=x2\left(2\right)\\m=5\left(loai\right)\end{matrix}\right.\)
thế(2) vào(1)=>\(x1=x2=1\left(4\right)\)
thế (4) vào (3)=>\(m-1=1=>m=2\left(TM\right)\)
vậy m=2 thì....

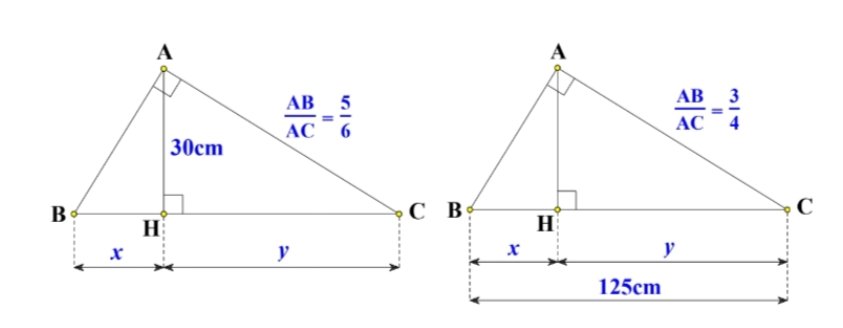
a: AB/AC=5/6
=>HB/HC=25/36
=>HB/25=HC/36=k
=>HB=25k; HC=36k
AH^2=HB*HC
=>25k*36k=30^2
=>900k^2=900
=>k=1
=>x=25cm; y=25cm
b: AB/AC=3/4
=>HB/HC=9/16
=>x/y=9/16
=>x/9=y/16=(x+y)/(9+16)=125/25=5
=>x=45cm; y=80cm


7:
a: \(P=\left(1:\dfrac{x-x+1}{\sqrt{x}+\sqrt{x-1}}-\dfrac{x-1-2}{\sqrt{x-1}-\sqrt{2}}\right)\cdot\left(\dfrac{2\sqrt{x}-\sqrt{x}-\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\right)\)\(=\left(\sqrt{x}+\sqrt{x-1}-\sqrt{x-1}-\sqrt{2}\right)\cdot\dfrac{\sqrt{x}-\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\)
\(=-\dfrac{\left(\sqrt{x}-\sqrt{2}\right)}{\sqrt{x}}\)
b: Khi x=3-2căn 2 thì \(P=-\dfrac{\sqrt{2}-1-\sqrt{2}}{\sqrt{2}-1}=\dfrac{1}{\sqrt{2}-1}=\sqrt{2}+1\)

bài 2:
b: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=4,8\left(cm\right)\\BH=3,6\left(cm\right)\\CH=6,4\left(cm\right)\end{matrix}\right.\)

Câu 2:
a: \(\Leftrightarrow\left(x^2+2x-15\right)\left(x^2+2x+1\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-3\right)\left(x+1\right)^2=0\)
hay \(x\in\left\{-5;-1;3\right\}\)
b: \(\Leftrightarrow\left(x^2-3x\right)^2-4x\left(x-3\right)+2x\left(x-3\right)-8=0\)
\(\Leftrightarrow x^2\left(x-3\right)^2-4x\left(x-3\right)+2x\left(x-3\right)-8=0\)
\(\Leftrightarrow x\left(x-3\right)\left(x^2-3x-4\right)+2\left(x^2-3x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+1\right)\left(x-1\right)\left(x-2\right)=0\)
hay \(x\in\left\{4;-1;1;2\right\}\)
c: \(\Leftrightarrow\left(x^2+x\right)^2+3\left(x^2+x\right)=0\)
=>x(x+1)=0
=>x=0 hoặc x=-1
\(a,\left(x^2+2x\right)^2-14\left(x^2+2x\right)-15=0\\ \Rightarrow\left[\left(x^2+2x\right)^2-15\left(x^2+2x\right)\right]+\left[\left(x^2+2x\right)-15\right]=0\\ \Rightarrow\left(x^2+2x\right)\left(x^2+2x-15\right)+\left(x^2+2x-15\right)=0\\ \Rightarrow\left(x^2+2x-15\right)\left(x^2+2x+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2+2x-15=0\\x^2+2x+1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x=-5\\x=-1\end{matrix}\right.\)

Câu 10: B
Câu 2:
1: b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2=-2x+5\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)


 giúp mình câu 4 với câu 2 phần 2 với
giúp mình câu 4 với câu 2 phần 2 với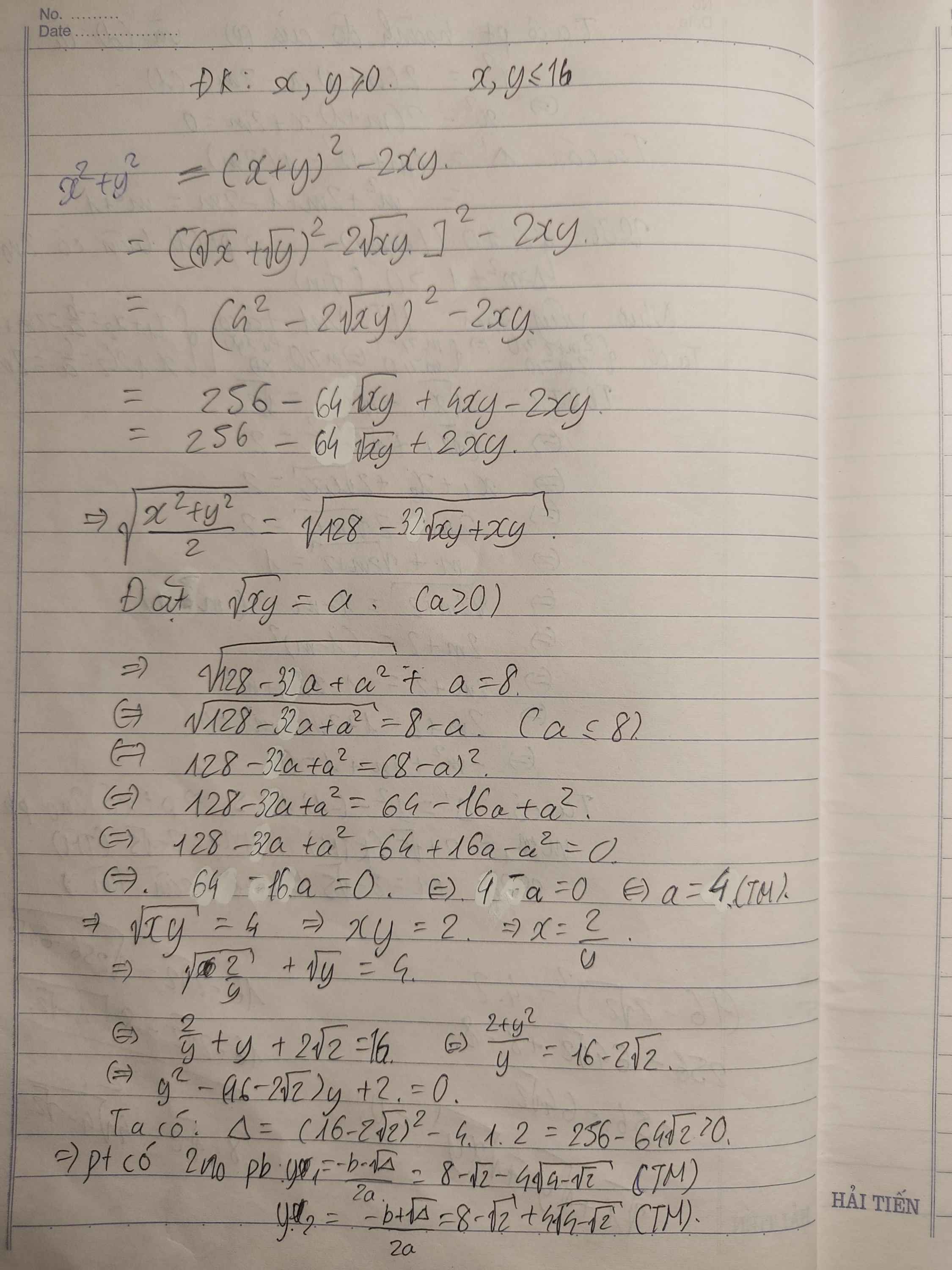
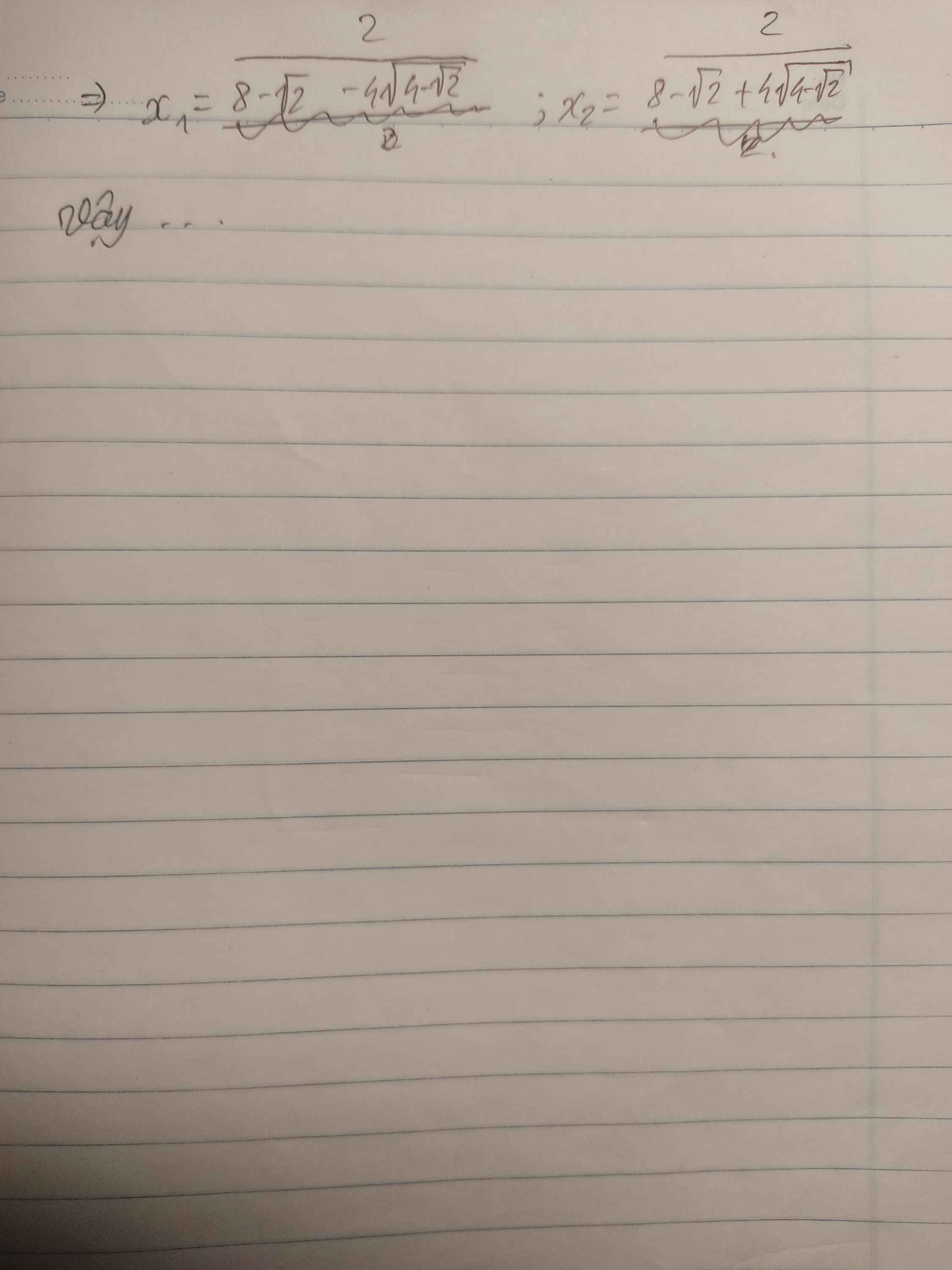

 Giúp mình giải 2 câu này với. Mình cảm ơn
Giúp mình giải 2 câu này với. Mình cảm ơn

 giải giúp mình câu 2 với
giải giúp mình câu 2 với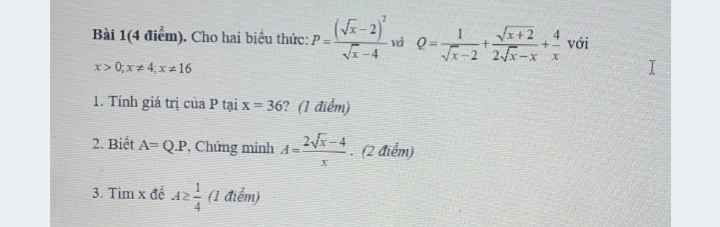
2:
PTHĐGĐ là:
x^2-5x+m+1=0
Δ=(-5)^2-4(m+1)
=25-4m-4=-4m+21
Để (P) cắt (d) tại hai điểm pb thì -4m+21>0
=>m<21/4
2x1=căn x2
=>x1>0 và x2=4x1^2
x1+x2=5
=>x2=5-x1
=>4x1^2=5-x1
=>x1=1
=>x2=4
x1+x2=m+1
=>m+1=4
=>m=3