Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) chu vi là:
[(0,5 + 0,1) + (0,2 + 0,03)] x 2 = 1,66 (m)
b) diện tích là:
(0,5 + 0,1) x (0,2 + 0,03) = 0,138 (m2)
Đ/s: a) 1,66 m
b) 0,138 m2

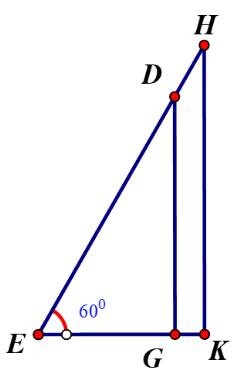
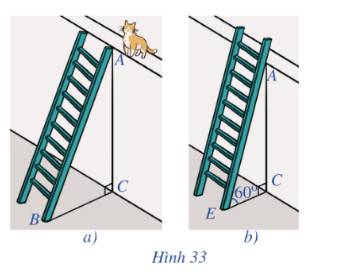
Gọi chiều cao bức tường DG là x (m) (x>0)
Chiều dài chiếc thang là x+1 (m)
Khoảng cách từ chân thang sau khi bác Nam điều chỉnh là: \(EG = \frac{{DG}}{{\sqrt 3 }} = \frac{{x\sqrt 3 }}{3}\) (m)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
\(BC = \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} \)(m)
Bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m nên ta có:
\(\sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} - 0,5 = \frac{{x\sqrt 3 }}{3}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} = \frac{x}{{\sqrt 3 }} + 0,5\\ \Leftrightarrow \sqrt {2x + 1} = \frac{x}{{\sqrt 3 }} + 0,5\left( * \right)\end{array}\)
Ta có \(\frac{x}{{\sqrt 3 }} + 0,5 \ge 0 \Leftrightarrow \frac{x}{{\sqrt 3 }} \ge - \frac{1}{2}\)\( \Leftrightarrow x \ge - \frac{{\sqrt 3 }}{2}\) (Luôn đúng do x>0)
Ta bình phương hai vế (*) ta được:
\(\begin{array}{l}2x + 1 = {\left( {\frac{x}{{\sqrt 3 }} + 0,5} \right)^2}\\ \Leftrightarrow 2x + 1 = \frac{{{x^2}}}{3} + \frac{x}{{\sqrt 3 }} + 0,25\\ \Leftrightarrow \frac{{{x^2}}}{3} + \left( {\frac{{\sqrt 3 }}{3} - 2} \right)x - \frac{3}{4} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x \approx 4,7\left( {tm} \right)\\x \approx - 0,5\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy chiều cao của bức tường là 4,7 m.


diện tích xung quanh căn nhà là:
(12+4)x2x3,5=112(m2)
diện tích quét sơn (không tính cửa sổ) là:
112-10,2=101,8(m2)
diện tích toàn bộ cần quét sơn là:
101,8+(3,5+2,5)x2x3,5=143,8(m2)
số tiền cần trả là:
143,8x20000=2876000(đồng)
đáp số: 2876000 đồng

\(\widehat{C}=90^0-35^0=55^0\)
XétΔABC vuông tại A có
\(AC=BC\cdot\sin B\)
nên \(BC=\dfrac{5}{\sin35^0}\simeq8.72\left(cm\right)\)
\(AB=\sqrt{8.72^2-5^2}=7.14\left(cm\right)\)

Ta có: \(P\left(x\right)=ax^3+bx^2+cx+d\)
*)Xét \(P\left(1\right)=a\cdot1^3+b\cdot1^2+c\cdot1+d=100\)
\(\Rightarrow a+b+c+d=100\)
*)Xét \(P\left(-1\right)=a\cdot\left(-1\right)^3+b\cdot\left(-1\right)^2+c\cdot\left(-1\right)+d=50\)
\(\Rightarrow-a+b-c+d=50\)
*)Xét \(P\left(0\right)=a\cdot0^3+b\cdot0^2+c\cdot0+d=1\)
\(\Rightarrow d=1\)
*)Xét \(P\left(2\right)=a\cdot2^3+b\cdot2^2+c\cdot2+d=120\)
\(\Rightarrow8a+4b+2c+d=120\)
Vậy ta có: \(\left\{{}\begin{matrix}a+b+c+d=100\\-a+b-c+d=50\\d=1\\8a+4b+2c+d=120\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{227}{6}\\b=74\\c=\dfrac{377}{6}\\d=1\end{matrix}\right.\)
Vậy đa thức \(P\left(x\right)=-\dfrac{227}{6}x^3+74x^2+\dfrac{377}{6}x+1\)
\(P\left(3\right)=-\dfrac{227}{6}\cdot3^3+74\cdot3^2+\dfrac{377}{6}\cdot3+1=-166\)
1. chú ý viết đề cẩn thận
2. đăng đúng box nó nhé cái nè để vào lớp 7

Thay ![]() = x ;
= x ; ![]() là y nhé bạn =='.
là y nhé bạn =='.
Theo đề bài ta có :
\(\left\{{}\begin{matrix}x+y=23\\x\cdot y=132\\y-x=1\end{matrix}\right.\left(ĐK:x,y>0\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=23-y\\x\cdot y=132\\y-\left(23-y\right)=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=23-y\\x\cdot y=132\\2y=24\Rightarrow y=12\end{matrix}\right.\)
Thay y = 12 vào hai đẳng thức trên ta được :
\(x+12=23\Rightarrow x=11\) hay \(x\cdot12=132\Rightarrow x=11\)
Vậy \(\left\{{}\begin{matrix}x=11\\y=12\end{matrix}\right.\) hay ![]() \(=11\);
\(=11\); ![]() \(=12\).
\(=12\).


Bạn vẽ cho mình cái hình minh họa đi. Chứ nói vầy mình không hiểu theo b thì như thế nào gọi là rõ nhất nữa
mình đâu biết vẽ hình đâu....vẽ hình ra thì chắc mình cũng biết làm
