Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,=\dfrac{\sqrt{2}\left(1+\sqrt{2}\right)}{1+\sqrt{2}}=\sqrt{2}\\ b,=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=\sqrt{5}\\ c,=\dfrac{\sqrt{3}\left(1-\sqrt{2}\right)}{2\left(\sqrt{2}-1\right)}=-\dfrac{\sqrt{3}}{2}\\ d,=\dfrac{\sqrt{5}\left(1-\sqrt{2}\right)}{\sqrt{3}\left(1-\sqrt{2}\right)}=\dfrac{\sqrt{5}}{\sqrt{3}}=\dfrac{\sqrt{15}}{3}\\ e,=\dfrac{\sqrt{7}\left(\sqrt{7}+1\right)}{\sqrt{7}+1}=\sqrt{7}\\ f,=\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}=\sqrt{5}\\ g,=\dfrac{\sqrt{2}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}=\sqrt{2}\\ h,=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=\sqrt{5}\)

Bài 5:
Xét ΔADC vuông tại D có DO là đường cao ứng với cạnh huyền AC
nên \(\left\{{}\begin{matrix}AD^2=AO\cdot AC\\DC^2=CO\cdot CA\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AO=7,2\left(cm\right)\\CO=12,8\left(cm\right)\end{matrix}\right.\)



1:
a: =>(x-1)(x-7)=0
=>x=1 hoặc x=7
b: =>x(x^2-9x+8)=0
=>x(x-1)(x-8)=0
=>\(x\in\left\{0;1;8\right\}\)
c: Đặt 1/căn x-7=a; 1/căn y+6=b
Theo đề, ta có:
7a-4b=5/3 và 5a+3b=13/6
=>a=1/3 và b=1/6
=>x-7=9 và y+6=36
=>x=16 và y=30
Bài 3:
a: Δ=(2m+3)^2-4(m^2+3m+2)
=4m^2+12m+9-4m^2-12m-8=1>0
=>PT luôn có hai nghiệm pb
b: x1^2+x2^2=1
=>(x1+x2)^2-2x1x2=1
=>(2m+3)^2-2(m^2+3m+2)=1
=>4m^2+12m+9-2m^2-6m-4-1=0
=>2m^2+6m+4=0
=>m=-1 hoặc m=-2

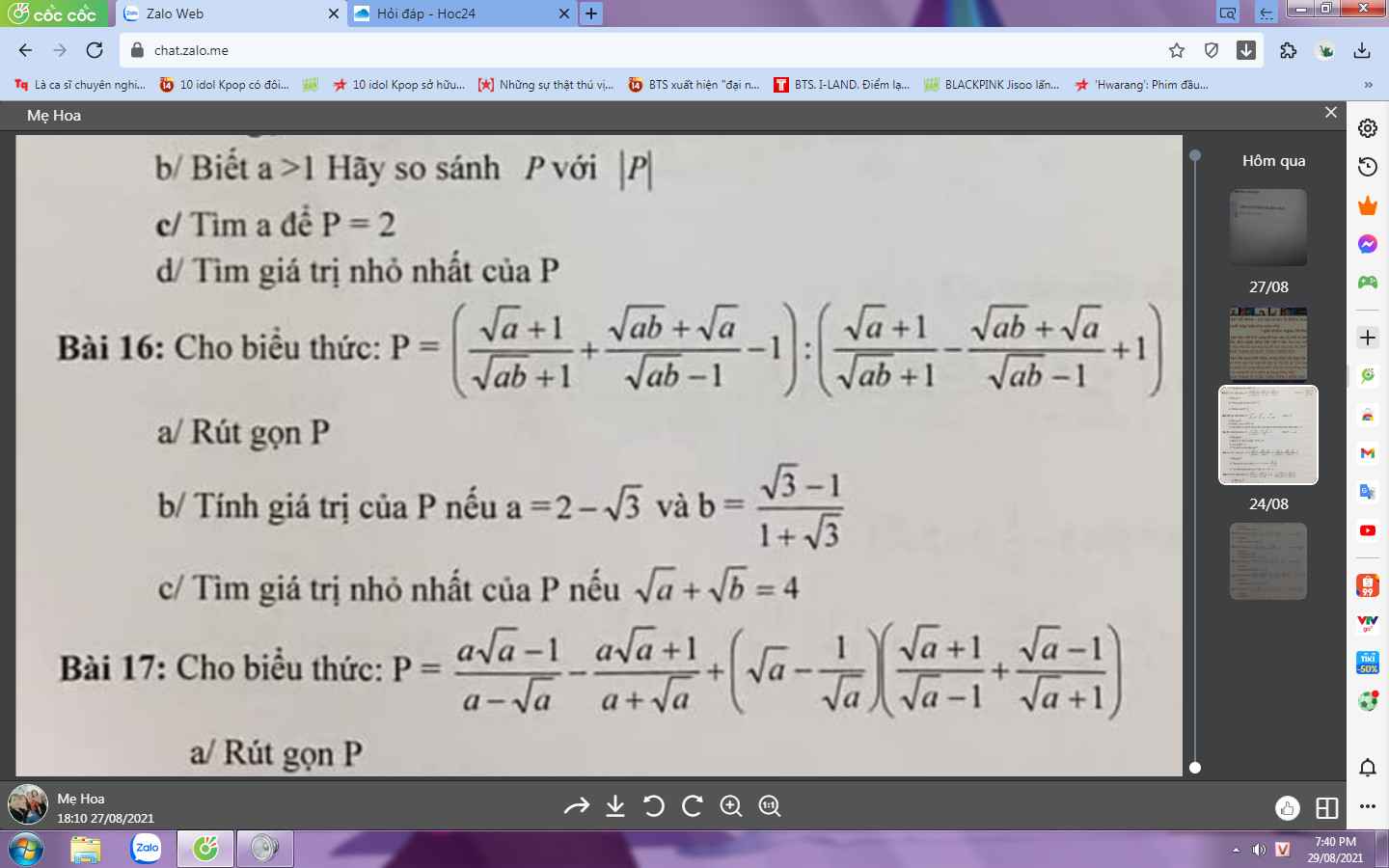
Bài 16:
a: Ta có: \(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}+\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}-1\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}-\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}+1\right)\)
\(=\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1+ab+\sqrt{ab}+a\sqrt{b}+\sqrt{a}-ab+1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}:\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1-ab-\sqrt{ab}-a\sqrt{b}-\sqrt{a}+ab-1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}\)
\(=\dfrac{2a\sqrt{b}+2\sqrt{ab}}{-2\sqrt{a}-2}\)
\(=\dfrac{2\sqrt{ab}\left(\sqrt{a}+1\right)}{-2\left(\sqrt{a}+1\right)}\)
\(=-\sqrt{ab}\)



 giúp mik vs mai mik phải nộp r giúp vs
giúp mik vs mai mik phải nộp r giúp vs