Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1:
\(A=\dfrac{2}{3}+\dfrac{8}{9}+...+\dfrac{3^n-1}{3^n}\)
\(=1-\dfrac{1}{3}+1-\dfrac{1}{3^2}+...+1-\dfrac{1}{3^n}\)
\(=n-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^n}\right)\)
Đặt \(B=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^n}\)
=>\(3B=1+\dfrac{1}{3^1}+...+\dfrac{1}{3^{n-1}}\)
=>\(2B=1+\dfrac{1}{3}+...+\dfrac{1}{3^{n-1}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^n}=1-\dfrac{1}{3^n}\)
=>\(2B=\dfrac{3^n-1}{3^n}\)
=>\(B=\dfrac{1}{2}-\dfrac{1}{2\cdot3^n}< \dfrac{1}{2}\)
\(A=n-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^n}\right)\)
\(=n-B>n-\dfrac{1}{2}\)

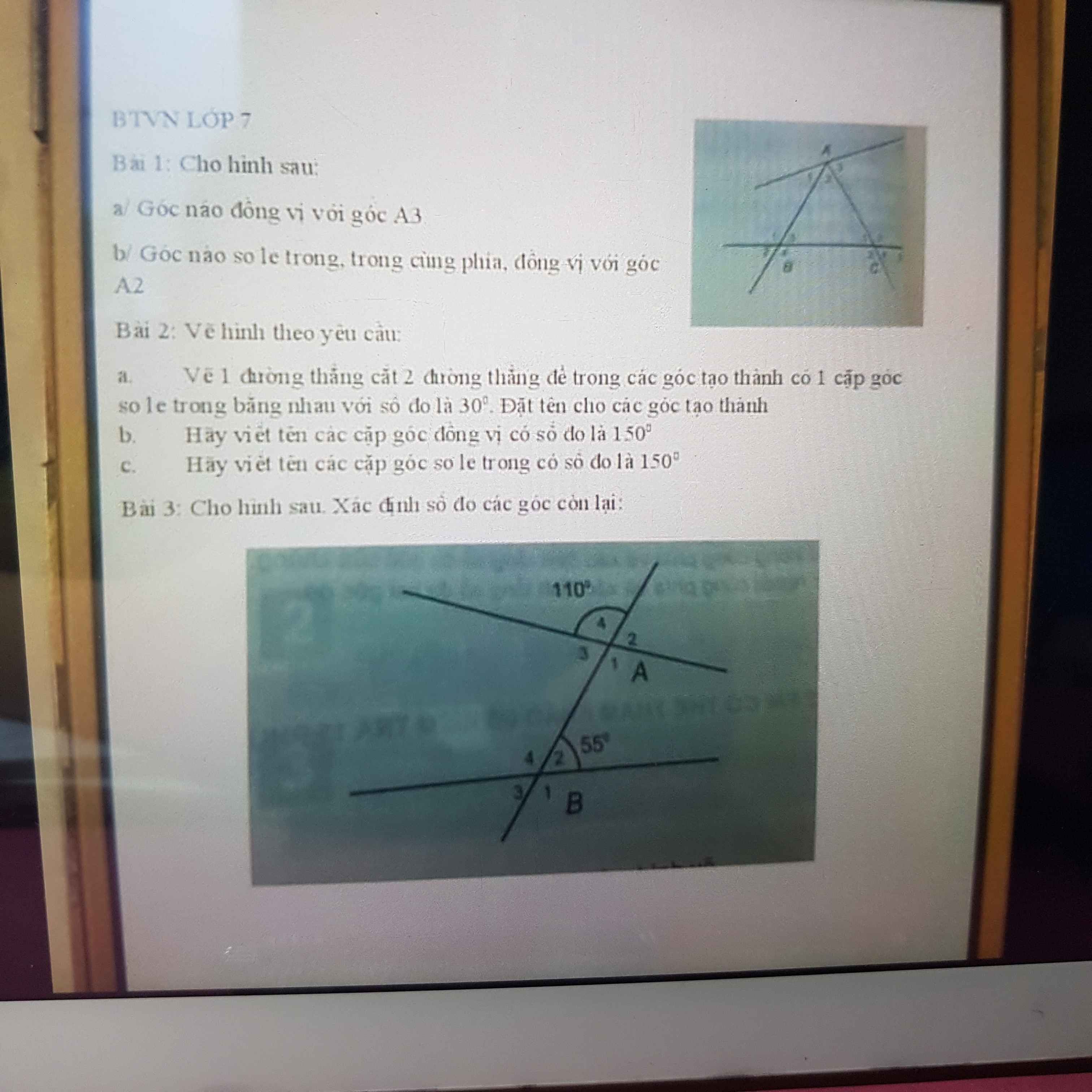
Bài 3:
\(\widehat{A_1}=110^0;\widehat{A_2}=70^0;\widehat{A_3}=70^0\)
\(\widehat{B_3}=55^0;\widehat{B_4}=125^0;\widehat{B_1}=125^0\)


4:
1: Xét ΔBMD vuông tại M và ΔBHD vuông tại H có
BD chung
góc MBD=góc HBD
=>ΔBMD=ΔBHD
2: Xét ΔDMA vuông tại M và ΔDHN vuông tại H có
DM=DH
góc ADM=góc HDN
=>ΔDMA=ΔDHN
=>DA=DN
=>ΔDAN cân tại D
góc CAN+góc BAN=90 độ
góc HAN+góc BNA=90 độ
mà góc BAN=góc BNA
nên góc CAN=góc HAN
=>AN là phân giác của góc HAC

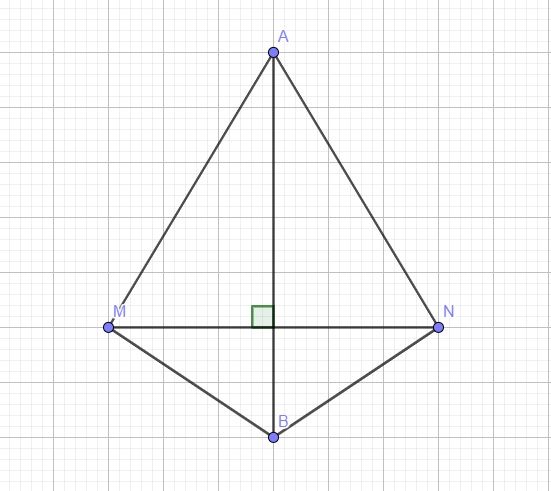
Do A thuộc trung trực đoạn MN nên \(AM=AN\)
Do B thuộc trung trực đoạn MN nên \(BM=BN\)
Xét 2 tam giác MAB và NAB có:
\(\left\{{}\begin{matrix}AM=AN\left(cmt\right)\\BM=BN\left(cmt\right)\\AB\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta MAB=\Delta NAB\left(c.c.c\right)\)

Bài 3:
a: Xét ΔCBA vuông tại B và ΔCHA vuông tại H có
CA chung
\(\widehat{BCA}=\widehat{HCA}\)
Do đó: ΔCBA=ΔCHA
Suy ra: CB=CH
hay ΔCBH cân tại C
b: Xét ΔBAF vuông tại B và ΔHAE vuông tại H có
AB=AH
\(\widehat{BAF}=\widehat{HAE}\)
Do đó: ΔBAF=ΔHAE
Suy ra: BF=HE
Xét ΔCFE có
CB/BF=CH/HE
nên BH//FE
c: Ta có: CF=CE
nên C nằm trên đường trung trực của EF(1)
Ta có: AF=AE
nên A nằm trên đường trung trực của FE(2)
Ta có: KF=KE
nên K nằm trên đường trung trực của FE(3)
Từ (1), (2) và (3) suy ra C,A,K thẳng hàng