
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.

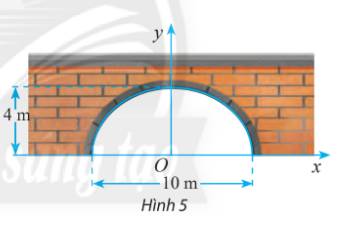
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)

\(A=\left(m-2;6\right),B=\left(-2;2m+2\right).\)
Để \(A,B\ne\varnothing\)
\(\Rightarrow\orbr{\begin{cases}m-2\ge-2\\2m+2>6\end{cases}}\Rightarrow\orbr{\begin{cases}m\ge0\\m>2\end{cases}}\)
Kết hợp ĐK \(2< m< 8\)
\(\Rightarrow m\in\left(2;8\right)\)

Từ giả thiết ta có:
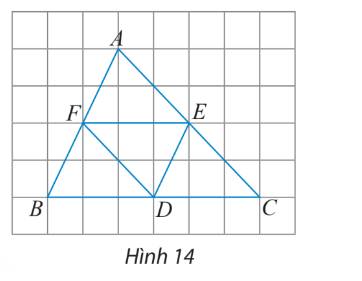
\(AF = FB = ED\); \(AE = EC = FD\); \(BD = DC = EF\)
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ \(\overrightarrow {EF} \)là \(\overrightarrow {DB} \) và \(\overrightarrow {CD} \)
b) Các vectơ đối vectơ \(\overrightarrow {EC} \) là \(\overrightarrow {EA} \) và \(\overrightarrow {DF} \)

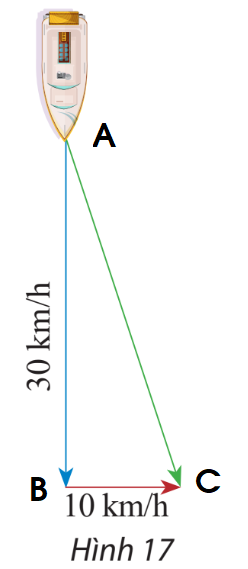
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).

Kết quả của mỗi lần thử là một cặp (i; j) với i và j lần lượt là số chấm xuất hiện trên hai xúc xắc, hai con xúc xắc gieo đồng thời nên không quan tâm thứ tự, ta có không gian mẫu là:
\(\Omega = \begin{array}{l}\{(1;1),(1;2),(1;3),(1;4),(1;5),(1;6),(2;2),(2;3),(2;4),(2;5),(2;6),(3;3),(3;4),(3;5),(3;6),\\(4;4),(4;5),(4;6),(5;5),(5;6),(6;6)\}\end{array} \)
Không gian mẫu gồm có 21 kết quả, tức là \(n\left( \Omega \right) = 21\)
a) Ta có tập hợp miêu tả biến cố A
\(A = \left\{ {(1;1),(2;2),(3;3),(4;4),(5;5),(6;6)} \right\} \Rightarrow n\left( A \right) = 6\)
Do đó, xác suất của biến cố A là: \(P\left( A \right) = \frac{{n(A)}}{{n(\Omega )}} = \frac{6}{{21}} = \frac{2}{7}\)
b) Ta có tập hợp miêu tả biến cố B
\(B = \left\{ {(6;3),(5;4)} \right\} \Rightarrow n\left( B \right) = 2\)
Do đó, xác suất của biến cố B là: \(P\left( B \right) = \frac{{n(B)}}{{n(\Omega )}} = \frac{2}{{21}}\)

a ) \mathbb{R} \backslash (-3; \, 1]R\(−3;1]=(-∞;-3]∪(1;+∞)
b) (-\infty; \, 1) \backslash [-2; \, 0](−∞;1)\[−2;0]=(- (-\infty; \, 1) \backslash [-2; \, 0]∞;-2)∪(0;1)
 giúp e với ạa
giúp e với ạa



a: 5 không là số nguyên tố
b: 4+x>=3
c: (căn 3+căn 12)^2 là số vô tỉ
d: Phương trình x^2+2023x=1 có nghiệm
e: 3^2+4^2<>5^2
f: căn 3*căn 27<>9
g: x=1 không là nghiệm của phương trình \(\dfrac{x^2-1}{x-1}=0\)
h: Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh còn lại