Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi B là biến cố: “Tổng số chấm xuất hiện trên bề mặt con súc sắc bằng 12”
Ta thấy
12 = 1 + 5 + 6 = 2 + 4 + 6 = 2 + 5 + 5 = 3 + 3 + 6 = 3 + 4 + 5 = 4 + 4 + 4
Nếu số chấm trên bề mặt 3 con súc sắc khác nhau tức là các trường hợp (1;5;6), (2;4;6), (3;4;5) có 3 ! .3 = 18 cách
Nếu số chấm trên bề mặt 3 con súc sắc có 2 con giống nhau tức là các trường hợp (2;5;5) và (3;3;6) có 3.2 = 6 cách
Nếu số chấm trên bề mặt 3 con súc sắc giống nhau ta có 1 cách gieo duy nhất
⇒ n B = 18 + 6 + 1 = 25 . Vậy P B = n B Ω B = 25 216 .
Chọn A

b) Biến cố A xảy ra khi mặt có số chấm không nhỏ hơn 2 xuất hiện
Vậy A={2,3,4,5,6}. Chọn phương án là C

a) Quan sát con súc sắc có 6 mặt ghi số chấm 1,2,3,4,5,6. Vì vậy không gian mẫu Ω={1,2,3,4,5,6}. Chọn đáp án D

Đáp án C
Gieo 2 lần ta có 36 kết quả, trong đó có 18 trường hợp ra tổng 2 lần chẵn, 18 trường hợp ra lẻ.
Đến lần gieo thứ 3, ta có
+) Nếu tổng 2 lần trước là chẵn, lần 3 là chẵn thì tổng 3 lần chẵn, suy ra có 3 kết quả
+) Nếu tổng 2 lần trước là lẻ, lần 3 là lẻ thì tổng 3 lần chẵn, suy ra có 3 kết quả
Với 18 lần chẵn và 18 lần được lẻ trong 2 lần gieo trước, số các kết quả thỏa mãn là 18.3 + 18.3 = 108.

Đáp án B
Phương pháp: Xác suất của biến cố A là n A n Ω trong đó nA là số khả năng mà biến cố A có thể xảy ra, n Ω là tất cả các khả năng có thể xảy ra.
Cách giải: x 2 + b x + c x + 1 = 0 (*)
Để phương trình (*) vô nghiệm thì phương trình x2 + bx + c = 0 (**) có 2 trường hợp xảy ra:
TH1: PT (**) có 1 nghiệm x = -1
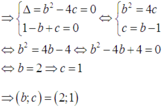
TH2: PT (**) vô nghiệm
![]()
Vì c là số chấm xuất hiện ở lần gieo thứ 2 nên c ≤ 6 ⇒ b ≤ 2 6 ≈ 4 , 9 .
Mà b là số chấm xuất hiện ở lần giao đầu nên b ∈ 1 ; 2 ; 3 ; 4
Với b = 1 ta có: c > 1 4 ⇒ c ∈ 1 ; 2 ; 3 ; 4 ; 5 ; 6 có 6 cách chọn c.
Với b = 2 ta có: c > 1 ⇒ c ∈ 2 ; 3 ; 4 ; 5 ; 6 có 5 cách chọn c.
Với b = 3 ta có: c > 9 4 ⇒ c ∈ 3 ; 4 ; 5 ; 6 có 4 cách chọn c.
Với b = 4 ta có: c > 4 => c ∈ 5 ; 6 có 2 cách chọn c.
Do đó có 6+5+4+2 = 17 cách chọn (b;c) để phương trình (**) vô nghiệm.
Gieo con súc sắc 2 lần nên số phần tử của không gian mẫu n Ω = 6 . 6 = 36
Vậy xác suất đề phương trình (*) vô nghiệm là 1 + 17 36 = 1 2

Không gian mẫu Ω = ( b , c ) : 1 ≤ b , c ≤ 6 . Kí hiệu A, B, C là các biến cố cần tìm xác suấtứng với các câu a), b), c). Ta có Δ = b 2 − 4 c
a)
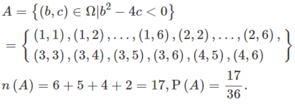
b)
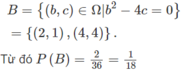
c)
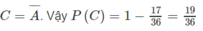

Đáp án là A.
• Số phần tử của không gian mẫu là n ( Ω ) = 36 .
Gọi A là biến cố thỏa yêu cầu bài toán.
Phương trình x2 + bx + c = 0 có nghiệm khi và chỉ khi ∆ = b 2 - 4 a c ≥ 0 ⇔ b 2 ≥ 4 a c .
Xét bảng kết quả (L – loại, không thỏa ; N – nhận, thỏa yêu cầu đề bài)

Đáp án A
![]() phương trình có 2 nghiệm
phương trình có 2 nghiệm ![]()
Phương trình có nghiệm lớn hơn 3 khi và chỉ khi
![]()
Suy ra xác suất để con súc sắc xuất hiện mặt b thỏa mãn đề bài là ![]()
a. Số khả năng xuất hiện S mỗi con xúc sắc là 6. Vì vậy số kết quả có thể xảy ra trên mặt xuất hiện của ba con xúc sắc là 6*6*6= 216
Chọn C