Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
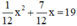
⇔ x2 + 7x = 228
⇔ x2 + 7x – 228 = 0
Có a = 1; b = 7; c = -228; Δ = b2 – 4ac = 72 – 4.1.(-228) = 961 > 0
Phương trình có hai nghiệm:
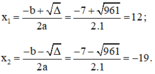
Vậy phương trình có hai nghiệm x1 = 12 và x2 = -19.
a) x 2 = 12 x + 288 ⇔ x 2 – 12 x – 288 = 0
Có a = 1; b’ = -6; c = -288; Δ ’ = b ’ 2 – a c = ( - 6 ) 2 – 1 . ( - 288 ) = 324 > 0
Phương trình có hai nghiệm:
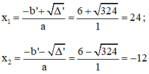
Vậy phương trình có hai nghiệm x 1 = 24 v à x 2 = - 12 .
b)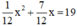 
⇔ x 2 + 7 x = 228 ⇔ x 2 + 7 x – 228 = 0
Có a = 1; b = 7; c = -228; Δ = b 2 – 4 a c = 7 2 – 4 . 1 . ( - 228 ) = 961 > 0
Phương trình có hai nghiệm:
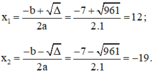
Vậy phương trình có hai nghiệm x 1 = 12 v à x 2 = - 19 .
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt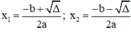 
+ Nếu Δ = 0, phương trình có nghiệm kép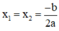 
;
+ Nếu Δ < 0, phương trình vô nghiệm.
* Về An-khô-va-ri-zmi (Muhammad inb Musa al – Khwarizmi):
An-khô-va-ri-zmi (780 – 850) là nhà toán học nổi tiếng người Trung Á.
Năm 820, ông viết một cuốn sách về Toán học, tên cuốn sách được dịch sang tiếng Anh với tiêu đề Algebra (dịch tiếng Việt là Đại số).
Ông được biết đến như là cha đẻ của môn Đại số. Ông dành cả đời mình nghiên cứu về đại số và đã có nhiều phát minh quan trọng trong lĩnh vực toán học.
Ngoài ra, ông cũng là nhà thiên văn học, địa lý học nổi tiếng và đóng góp một phần quan trọng trong việc vẽ bản đồ thế giới thời bấy giờ.
a) x2 = 12x + 288 ⇔ x2 - 12x + 288 = 0
∆’ = (-6)2 – 1 . (-288) = 36 + 288 = 324
√∆’ = 18
x1 = 6 + 18 = 24, x2 = 6 – 18 = -12
b) x2 +
x = 19
⇔ x2 + 7x – 228 = 0, ∆ = 49 – 4 . (-228) = 49 + 912 = 961 = 312
x1 = = 12, x2 =
= -19
\(\dfrac{x^2-26}{10}+\dfrac{x^2-25}{11}\ge\dfrac{x^2-24}{12}+\dfrac{x^2-23}{13}\)
\(\Leftrightarrow\left(\dfrac{x^2-26}{10}-1\right)+\left(\dfrac{x^2-25}{11}-1\right)\ge\left(\dfrac{x^2-24}{12}-1\right)+\left(\dfrac{x^2-23}{13}-1\right)\)
\(\Leftrightarrow\dfrac{x^2-36}{10}+\dfrac{x^2-36}{11}\ge\dfrac{x^2-36}{12}+\dfrac{x^2-36}{13}\)
\(\Leftrightarrow\dfrac{x^2-36}{10}+\dfrac{x^2-36}{11}-\dfrac{x^2-36}{12}-\dfrac{x^2-36}{13}\ge0\)
\(\Leftrightarrow\left(x^2-36\right)\left(\dfrac{1}{10}+\dfrac{1}{11}-\dfrac{1}{12}-\dfrac{1}{13}\right)\ge0\)
Vì \(\dfrac{1}{10}+\dfrac{1}{11}-\dfrac{1}{12}-\dfrac{1}{13}>0\Rightarrow x^2-36\ge0\Leftrightarrow\left[{}\begin{matrix}x\le-6\\x\ge6\end{matrix}\right.\)
Bất phương trình đó tương đương với:
\(\left(\dfrac{x^2-26}{10}-1\right)+\left(\dfrac{x^2-25}{11}-1\right)\ge\left(\dfrac{x^2-24}{12}-1\right)+\left(\dfrac{x^2-23}{13}-1\right)\)
⇔ \(\dfrac{x^2-36}{10}+\dfrac{x^2-36}{11}\ge\dfrac{x^2-36}{12}+\dfrac{x^2-36}{13}\)
⇔ \(\dfrac{x^2-36}{10}+\dfrac{x^2-36}{11}-\dfrac{x^2-36}{12}-\dfrac{x^2-36}{13}\ge0\)
⇔ \(\left(x^2-36\right)\left(\dfrac{1}{10}+\dfrac{1}{11}-\dfrac{1}{12}-\dfrac{1}{13}\right)\ge0\)
+)Vì \(\dfrac{1}{10}>\dfrac{1}{11}>\dfrac{1}{12}>\dfrac{1}{13}\) nên \(\dfrac{1}{10}+\dfrac{1}{11}-\dfrac{1}{12}-\dfrac{1}{13}>0\)
⇔ \(x^2-36\ge0\)
⇔ \(x^2\ge36\)
⇔ \(\sqrt{x^2}\ge6\)
⇔ \(\left|x\right|\ge6\)
⇔ \(\left[{}\begin{matrix}x\ge6\\x\le-6\end{matrix}\right.\)
➤ Vậy \(\left[{}\begin{matrix}x\ge6\\x\le-6\end{matrix}\right.\)
ĐKXĐ: \(x\ge0\)
\(x^2+\sqrt{x}+7=7\\ x^2+\sqrt{x}=0\\ \sqrt{x}\left(x\sqrt{x}+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}\sqrt{x}=0\\x\sqrt{x}=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x\in\varnothing\end{matrix}\right.\)
vậy phương trình có tập nghiệm là S={0}
\(PT\Leftrightarrow x^2-2x+\sqrt{6x^2-12x+7}=0\\ \Leftrightarrow x^2-2x+1+\sqrt{6x^2-12x+7}-1=0\\ \Leftrightarrow\left(x-1\right)^2+\dfrac{6\left(x-1\right)^2}{\sqrt{6x^2-12x+7}+1}=0\\ \Leftrightarrow\left(x-1\right)\left(x-1+\dfrac{6}{\sqrt{6x^2-12x+7}+1}\right)=0\\ \Leftrightarrow x=1\left(x-1+\dfrac{6}{\sqrt{6x^2-12x+7}+1}>0\right)\)
x2 = 12x + 288
⇔ x2 – 12x – 288 = 0
Có a = 1; b’ = -6; c = -288; Δ’ = b’2 – ac = (-6)2 – 1.(-288) = 324 > 0
Phương trình có hai nghiệm:
Vậy phương trình có hai nghiệm x1 = 24 và x2 = -12.