
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/
\(\Leftrightarrow3cos^2x-4sinx.cosx+1-cos^2x=1\)
\(\Leftrightarrow2cos^2x-4sinx.cosx=0\)
\(\Leftrightarrow2cosx\left(cosx-2sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\tanx=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=arctan\left(\frac{1}{2}\right)+k\pi\end{matrix}\right.\)
b.
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^2x\)
\(4-3tanx+3tan^2x=1+tan^2x\)
\(\Leftrightarrow2tan^2x-3tanx+3=0\)
Pt vô nghiệm

\(sin^2x+sin^22x=1\)
\(\Leftrightarrow2sin^2x-1+2sin^22x-2=-1\)
\(\Leftrightarrow-cos2x-2cos^22x+1=0\)
\(\Leftrightarrow\left(cos2x+1\right)\left(2cos2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-1\\cos2x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\pi+k2\pi\\2x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)

\(cos^2x-sin2x-sin^2x=1\)
\(\Leftrightarrow1-sin^2x-2sinx.cosx-sin^2x=1\)
\(\Leftrightarrow sin^2x+sinx.cosx=0\)
\(\Leftrightarrow sinx\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\tanx=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)


b) \(2sin^2x-3sinxcosx+cos^2x=0\)
\(\Leftrightarrow2tan^2x-3tanx+1=0\left(cosx\ne0\Leftrightarrow x\ne\dfrac{\pi}{2}+k\pi\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=tan\dfrac{\pi}{4}\\tanx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{1}{2}\right)+k\pi\end{matrix}\right.\left(k\in Z\right)\)

b)
(sin2x + cos2x)cosx + 2cos2x - sinx = 0
⇔ cos2x (cosx + 2) + sinx (2cos2 x – 1) = 0
⇔ cos2x (cosx + 2) + sinx.cos2x = 0
⇔ cos2x (cosx + sinx + 2) = 0
⇔ cos2x = 0
⇔ 2x = 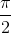 + kπ ⇔ x =
+ kπ ⇔ x = 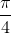 + k
+ k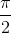 (k ∈
(k ∈ 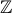 )
)
c)
Đáp án:
x=π6π6+ k2ππ
và x= 5π65π6+k2ππ (k∈Z)
Lời giải:
sin2x-cos2x+3sinx-cosx-1=0
⇔ 2sinxcosx-(1-2sin²x) +3sinx-cosx-1=0
⇔ 2sin²x+2sinxcosx+3sinx-cosx-2=0
⇔ (2sin²x+3sinx-2)+ cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+2)+cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+cosx+2)=0
⇔ sinx=1212
⇔ x=π6π6+ k2ππ
hoặc x= 5π65π6+k2ππ (k∈Z)
(sinx+cosx+2)=0 (vô nghiệm do sinx+cosx+2=√22sin(x+π4π4)+2>0)

Với \(sinx=0\) không phải nghiệm (vế trái bằng 9, vế phải hiển nhiên nhỏ hơn 9)
Với \(sinx\ne0\):
\(\Rightarrow\left(3sinx-4sin^3x\right)\left(3-4sin^23x\right)=sinx-2sinx.cos10x\)
\(\Leftrightarrow sin3x\left(3-4sin^23x\right)=sinx-2sinx.cos10x\)
\(\Leftrightarrow3sin3x-4sin^33x=sinx-sin11x+sin9x\)
\(\Leftrightarrow sin9x=sinx-sin11x+sin9x\)
\(\Leftrightarrow sin11x=sinx\)
\(\Leftrightarrow...\)

- Với \(cosx=0\) không phải nghiệm
- Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\) ta được:
\(tan^2x-3tanx=-\dfrac{1}{cos^2x}\)
\(\Leftrightarrow tan^2x-3tanx=-1-tan^2x\)
\(\Leftrightarrow2tan^2x-3tanx+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{1}{2}\right)+k\pi\end{matrix}\right.\)
Em muốn hỏi chút là tại sao lại biết cosx = 0 không phải nghiệm ạ? Có phải trình bày roc ra không hay chỉ viết là cosx = 0 không phải nghiệm ạ?