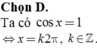
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
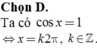
ĐKXĐ: ...
\(sin3x-cos3x+sinx+cosx=\dfrac{sin3x-cos3x+sinx+cosx}{\left(sin3x+cosx\right)\left(cos3x-sinx\right)}\)
\(\Rightarrow\left[{}\begin{matrix}sin3x-cos3x+sinx+cosx=0\left(1\right)\\\left(sin3x+cosx\right)\left(cos3x-sinx\right)=1\left(2\right)\end{matrix}\right.\)
(1) \(\Leftrightarrow3sinx-4sin^3x-4cos^3x+3cosx+sinx+cosx=0\)
\(\Leftrightarrow sinx+cosx+sin^3x+cos^3x=0\)
\(\Leftrightarrow sinx+cosx+\left(sinx+cosx\right)\left(1-sinx.cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(2-sinx.cosx\right)=0\)
\(\Leftrightarrow sinx+cosx=0\) (loại)
(2) \(\Leftrightarrow sin3x.cos3x-sinx.cosx-sin3x.sinx+cos3x.cosx=1\)
\(\Leftrightarrow\dfrac{1}{2}sin6x-\dfrac{1}{2}sin2x+cos4x=1\)
\(\Leftrightarrow\dfrac{1}{2}\left(3sin2x-4sin^32x\right)-\dfrac{1}{2}sin2x+1-2sin^22x=1\)
\(\Leftrightarrow sin2x-2sin^32x-2sin^22x=0\)
\(\Leftrightarrow-sin2x\left(2sin^22x+2sin2x-1\right)=0\)
\(\Leftrightarrow...\)
2.1
a.
\(\Leftrightarrow sinx-cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k2\pi\\x=\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
b.
\(cosx-\sqrt{3}sinx=1\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
2.sin x + cos x = 1
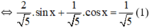
Vì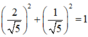 
nên tồn tại α thỏa mãn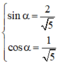 
(1) trở thành:
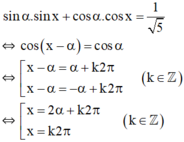
Vậy phương trình có nghiệm {k2π; 2α+k2π/k ∈ Z }
với α thỏa mãn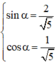 
-1/2 = cos 2π/3 nên cos x = (-1)/2
⇔ cos x = cos 2π/3
⇔ x = ±2π/3 + k2π, k ∈ Z
=>cosx=pi/2+k2pi
Phương trình này sẽ có nghiệm khi -1<=pi/2+k2pi<=1 và k thuộc Z
=>\(x\in\varnothing\)
\(cos2x+cosx+1=sin2x+sinx\)
\(\Leftrightarrow cos^2x-sin^2x+cosx+cos^2x+sin^2x=2sinx.cosx+sinx\)
\(\Leftrightarrow2cos^2x+cosx=2sinx.cosx+sinx\)
\(\Leftrightarrow cosx\left(2cosx+1\right)=sinx\left(2cosx+1\right)\)
\(\Leftrightarrow\left(2cosx+1\right)\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2cosx+1=0\\sinx=cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}cosx=-\dfrac{1}{2}\\tanx=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm\dfrac{\pi}{3}+k2\pi\\x=\dfrac{\pi}{4}+k\pi\\\end{matrix}\right.\)
