K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 7 2021
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}+k2\pi\\x\ne-\dfrac{\pi}{6}+k2\pi\\x\ne\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\dfrac{cosx-2sinx.cosx}{1-2sin^2x+sinx}=\sqrt{3}\)
\(\Leftrightarrow\dfrac{cosx-sin2x}{cos2x+sinx}=\sqrt{3}\)
\(\Rightarrow cosx-sin2x=\sqrt{3}cos2x+\sqrt{3}sinx\)
\(\Leftrightarrow cosx-\sqrt{3}sinx=\sqrt{3}cos2x+sin2x\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{\sqrt{3}}{2}cos2x+\dfrac{1}{2}sin2x\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=cos\left(2x-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{6}=x+\dfrac{\pi}{3}+k2\pi\\2x-\dfrac{\pi}{6}=-x-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\left(loại\right)\\x=-\dfrac{\pi}{18}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
KB
17 tháng 7 2021
ĐKXĐ : \(sinx\ne1;-\dfrac{1}{2}\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}+2k\pi\\x\ne\dfrac{-\pi}{6}+2k\pi;\dfrac{7\pi}{6}+2k\pi\end{matrix}\right.\)
\(\Leftrightarrow x\ne\dfrac{-\pi}{6}+\dfrac{2}{3}k\pi\)( k thuộc Z )
P/t đã cho \(\Leftrightarrow\dfrac{cosx-sin2x}{1-2sin^2x+sinx}=\sqrt{3}\)
\(\Leftrightarrow cosx-sin2x=\sqrt{3}\left(cos2x+sinx\right)\)
\(\Leftrightarrow cosx-\sqrt{3}sinx=\sqrt{3}cos2x+sin2x\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{\sqrt{3}}{2}cos2x+\dfrac{1}{2}sin2x\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=cos\left(2x+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{6}=x+\dfrac{\pi}{3}+2k\pi\\2x+\dfrac{\pi}{6}=-x-\dfrac{\pi}{3}+2k\pi\end{matrix}\right.\) ( k thuộc Z )
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+2k\pi\\x=\dfrac{-\pi}{6}+\dfrac{2}{3}k\pi\left(L\right)\end{matrix}\right.\)
Vậy ...
AH
Akai Haruma
Giáo viên
24 tháng 7 2021
Lời giải:
PT $\Leftrightarrow (2\cos x-1)(2\sin x+\cos x)=2\sin x\cos x-\sin x$
$\Leftrightarrow (2\cos x-1)(2\sin x+\cos x)=\sin x(2\cos x-1)$
$\Leftrightarrow (2\cos x-1)(\sin x+\cos x)=0$
$\Rightarrow 2\cos x=1$ hoặc $\sin x=-\cos x=\cos (\pi -x)=\sin (x-\frac{\pi}{2})$
Đến đây thì đơn giản rồi.
AH
Akai Haruma
Giáo viên
24 tháng 7 2021
Nkjuiopmli Sv5: Bạn chuyển vế sin x(2cos x-1) sang vế trái thì vế phải còn 0 đó.
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
2.1
a.
\(\Leftrightarrow sinx-cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k2\pi\\x=\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
b.
\(cosx-\sqrt{3}sinx=1\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
CM
15 tháng 6 2017
Đặt t = sin x + cos x = 2 sin x + π 4
Vì sin x + π 4 ∈ − 1 ; 1 ⇒ t ∈ − 2 ; 2
Ta có t 2 = sin x + cos x 2 = sin 2 x + cos 2 x + 2 sin x cos x ⇒ sin x cos x = t 2 − 1 2 .
Khi đó, phương trình đã cho trở thành:
t 2 − 1 2 + 2 t = 2 ⇔ t 2 + 4 t − 5 = 0 ⇔ t = 1 t = − 5 l .
Với t = 1, ta được sin x + cos x = 1 ⇔ sin x + π 4 = 1 2 ⇔ sin x + π 4 = sin π 4 .
⇔ x + π 4 = π 4 + k 2 π x + π 4 = π − π 4 + k 2 π ⇔ x = k 2 π x = π 2 + k 2 π , k ∈ ℤ
Chọn đáp án B.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 9 2019
a/ ĐKXĐ: \(\left\{{}\begin{matrix}sinx\ne1\\sinx\ne-\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne\frac{\pi}{2}+k2\pi\\x\ne-\frac{\pi}{6}+k2\pi\\x\ne\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow cosx-sin2x=\sqrt{3}\left(1+sinx-2sin^2x\right)\)
\(\Leftrightarrow cosx-sin2x=\sqrt{3}\left(cos2x+sinx\right)\)
\(\Leftrightarrow\sqrt{3}sinx-cosx=sin2x+\sqrt{3}cos2x\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}sinx-\frac{1}{2}cosx=\frac{1}{2}sin2x+\frac{\sqrt{3}}{2}cos2x\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{3}\right)=sin\left(2x+\frac{\pi}{6}\right)\)
\(\Leftrightarrow...\)
b/ ĐKXĐ: \(cosx+\sqrt{3}sinx\ne0\Leftrightarrow sin\left(x+\frac{\pi}{6}\right)\ne0\Rightarrow...\)
Đặt \(cosx+\sqrt{3}sinx=2sin\left(x+\frac{\pi}{6}\right)=a\) với \(-2\le a\le2\):
\(a=\frac{3}{a}+1\Leftrightarrow a^2-a-3=0\)
\(\Rightarrow\left[{}\begin{matrix}a=\frac{1+\sqrt{13}}{2}>2\left(l\right)\\a=\frac{1-\sqrt{13}}{2}\end{matrix}\right.\)
\(\Rightarrow2sin\left(x+\frac{\pi}{6}\right)=\frac{1-\sqrt{13}}{2}\)
\(\Rightarrow sin\left(x+\frac{\pi}{6}\right)=\frac{1-\sqrt{13}}{4}=sin\alpha\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{\pi}{6}=\alpha+k2\pi\\x+\frac{\pi}{6}=\pi-\alpha+k2\pi\end{matrix}\right.\) \(\Rightarrow x=...\)
MN
Giải phương trình: \(\frac{cosx\left(cosx+2sinx\right)+3sinx\left(sĩn+\sqrt{2}\right)}{2sinx-1}\)= 1
2
MN
19 tháng 6 2020
Cái chỗ biến đổi tương đương cuối cùng bạn làm rõ chút dc ko???
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 6 2020
Ném đoạn \(2sin^2x+\left(3\sqrt{2}-2\right)sinx+1\) vào casio mà bấm pt bậc 2 thôi, nó sẽ tách ra biểu thức như cái cuối cùng
Hoặc là tách thế này:
\(2sin^2x+\left(3\sqrt{2}-2\right)sinx+1\)
\(=2\left[sin^2x-2.\frac{2-3\sqrt{2}}{4}sinx+\left(\frac{2-3\sqrt{2}}{4}\right)^2-\left(\frac{2-3\sqrt{2}}{4}\right)^2\right]+1\)
\(=2\left(sinx-\frac{2-3\sqrt{2}}{4}\right)^2-2\left(\frac{2-3\sqrt{2}}{4}\right)^2+1\)
\(=2\left(sin^2x-\frac{2-3\sqrt{2}}{4}\right)^2+\frac{6\sqrt{2}-7}{4}\)
Với lưu ý \(\frac{6\sqrt{2}-7}{4}>0\) nên biểu thức luôn dương
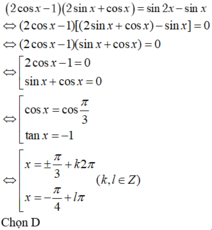
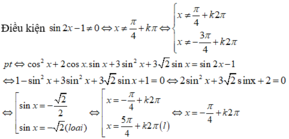
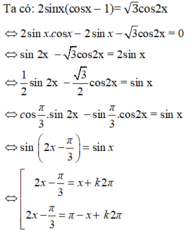
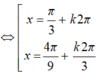
2.sin x + cos x = 1
Vì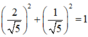
nên tồn tại α thỏa mãn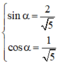 
(1) trở thành:
Vậy phương trình có nghiệm {k2π; 2α+k2π/k ∈ Z }
với α thỏa mãn