K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 7 2017
Ta có : 17 - 14(x + 1) = 13 - 4(x + 1) - 5(x - 3)
<=> 17 - 14x - 14 = 13 - 4x - 4 - 5x + 15
<=> -14x + 3 = -9x + 24
<=> -14x + 9x = 24 - 3
<=> -5x = 21
=> x = -4,2
1 tháng 7 2017
Ta có : 5x + 3,5 + (3x - 4) = 7x - 3(x - 0,5)
<=> 5x + 3,5 + 3x - 4 = 7x - 3x + 1,5
<=> 8x - 0,5 = 4x + 1,5
=> 8x - 4x = 1,5 + 0,5
=> 4x = 2
=> x = \(\frac{1}{2}\)
NT
2
18 tháng 5 2018
Bình phương 2 vế lên là giải được bạn nhé !
3x2 + 5x + 14 = 5(x + 1)\(\sqrt{4x-1}\)
<=> \(\left(3x^2+5x+14\right)^2=\left[5\left(x+1\right)\sqrt{4x-1}\right]^2\)
Phân tích ra giải tiếp nhé bạn
18 tháng 5 2018
Nếu phân tích ra tiếp sẽ ra phương trình bậc 4, PT ấy k có nghiệm nguyên
KT
28 tháng 4 2018
Nếu \(x^2-9x+14=\left(x-7\right)\left(x-2\right)\ge0\)
\(\Leftrightarrow\)\(x\ge7;\)\(x\le2\)
thì \(\left|x^2-9x+14\right|=x^2-9x+14\)
Khi đó bpt trở thành: \(x^2-9x+14+3x>x^2-4\)
\(\Leftrightarrow\)\(-6x>-18\)
\(\Leftrightarrow\) \(x< 3\)(thỏa mãn)
Nếu \(x^2-9x+14=\left(x-7\right)\left(x-2\right)< 0\)
\(\Leftrightarrow\)\(2< x< 7\)
thì \(\left|x^2-9x+14\right|=-x^2+9x-14\)
Khi đó bpt trở thành: \(-x^2+9x-14+3x>x^2-4\)
\(\Leftrightarrow\)\(-2x^2+12x-10>0\)
\(\Leftrightarrow\) \(x^2-6x+5< 0\)
\(\Leftrightarrow\)\(\left(x-1\right)\left(x-5\right)< 0\)
\(\Leftrightarrow\) \(1< x< 5\) (thỏa mãn)
Vậy...
4 tháng 5 2017
1/a/\(\Leftrightarrow\left(x+5\right)\left(x+6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\x+6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=-6\end{cases}}}\)
Vậy ...................
b/ ĐKXĐ:\(x\ne2;x\ne5\)
.....\(\Rightarrow3x^2-15x-x^2+2x+3x=0\)
\(\Leftrightarrow2x^2-10x=0\)
\(\Leftrightarrow2x\left(x-5\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}2x=0\\x-5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\left(nhận\right)\\x=5\left(loại\right)\end{cases}}}\)
Vậy ..............
YN
24 tháng 2 2022
`Answer:`
`1.`
a. \(\left(x+5\right)\left(2x+1\right)-x^2+25=0\)
\(\Leftrightarrow\left(x+5\right)\left(2x+1\right)-\left(x^2-25\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(2x+1\right)-\left(x+5\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(2x+1-x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x+6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\x+6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-6\\x=-5\end{cases}}}\)
b. \(\frac{3x}{x-2}-\frac{x}{x-5}+\frac{3x}{\left(x-2\right)\left(x-5\right)}=0\left(ĐKXĐ:x\ne2;x\ne5\right)\)
\(\Leftrightarrow\frac{3x\left(x-5\right)}{\left(x-2\right)\left(x-5\right)}-\frac{x\left(x-2\right)}{\left(x-2\right)\left(x-5\right)}+\frac{3x}{\left(x-2\right)\left(x-5\right)}=0\)
\(\Leftrightarrow\frac{3x\left(x-5\right)-x\left(x-2\right)+3x}{\left(x-2\right)\left(x-5\right)}=0\)
\(\Leftrightarrow3x\left(x-5\right)-x\left(x-2\right)+3x=0\)
\(\Leftrightarrow3x^2-15x-x^2+2x+3x=0\)
\(\Leftrightarrow2x\left(x-5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x=0\\x-5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=5\text{(Không thoả mãn)}\end{cases}}}\)
`2.`
\(ĐKXĐ:x\ne-m-2;x\ne m-2\)
Ta có: \(\frac{x+1}{x+2+m}=\frac{x+1}{x+2-m}\left(1\right)\)
a. Khi `m=-3` phương trình `(1)` sẽ trở thành: \(\frac{x+1}{x-1}=\frac{x+1}{x+5}\left(x\ne1;x\ne-5\right)\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\\frac{1}{x-1}=\frac{1}{x+5}\end{cases}\Leftrightarrow\orbr{\begin{cases}x+1=0\\x-1=x+5\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1\\-1=5\text{(Vô nghiệm)}\end{cases}}}\)
b. Để phương trình `(1)` nhận `x=3` làm nghiệm thì
\(\Leftrightarrow\hept{\begin{cases}\frac{3+1}{3+2-m}=\frac{3+1}{3+2-m}\\3\ne-m-2\\3\ne m-2\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{4}{5+m}=\frac{4}{5-m}\\m\ne\pm5\end{cases}}\Leftrightarrow\hept{\begin{cases}5+m=5-m\\m\ne\pm5\end{cases}}\Leftrightarrow m=0\)
DD
0
NT
1
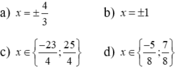
Xét : \(x\ge\dfrac{14}{3}\Rightarrow3x-14-x-2=5\Leftrightarrow2x=21\Leftrightarrow x=\dfrac{21}{2}\)
Xét : \(-2\le0< \dfrac{14}{3}\Rightarrow14-3x-x-2=5\Leftrightarrow-4x=-7\Leftrightarrow x=\dfrac{7}{4}\)