Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2.
\(0\le\left|sinx\right|\le1\Rightarrow1\le y\le3\)
Min và max lần lượt là 3 và 1
3.
\(cos\left(x-\frac{\pi}{2}\right)\le1\Rightarrow y\le3.1+1=4\)
8.
\(y=\frac{1}{2}+\frac{1}{2}cos2x+2cos2x=\frac{1}{2}+\frac{5}{2}cos2x\le\frac{1}{2}+\frac{5}{2}.1=3\)
15.
Nó đi qua vô số điểm nên ko có 4 đáp án để chọn thì ko ai có thể trả lời câu này cho bạn cả
18.
\(y=\frac{sinx+2cosx+1}{sinx+cosx+2}\Leftrightarrow y.sinx+y.cosx+2y=sinx+2cosx+1\)
\(\Leftrightarrow\left(y-1\right)sinx+\left(y-2\right)cosx=1-2y\)
\(\left(y-1\right)^2+\left(y-2\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow2y^2+2y-4\le0\Rightarrow-2\le y\le1\)
\(\Rightarrow y_{max}=1\)


\(y=3\left(cosx-\frac{1}{3}\right)^2+\frac{8}{3}\ge\frac{8}{3}\)
\(y_{min}=\frac{8}{3}\) khi \(cosx=\frac{1}{3}\)
\(y=8+\left(3cos^2x-2cosx-5\right)=8+\left(cosx+1\right)\left(3cosx-5\right)\le8\)
\(y_{max}=8\) khi \(cosx=-1\)

\(0\le sin^23x\le1\Rightarrow3\le y\le4\)
\(y_{min}=3\) khi \(sin^23x=1\Rightarrow x=\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
\(y_{max}=4\) khi \(sin^23x=0\Rightarrow x=\dfrac{k\pi}{3}\)

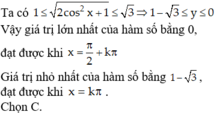
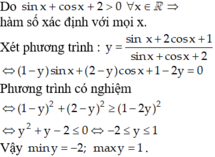
vì -1 ≤ cos(3x) ≤ 1 nên 0 ≤ cos2(3x) ≤ 1
⇒ max = 1 khi cos2(3x) = 0 ⇔ x = \(\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
min = -2 khi cos2(3x) = 1 ⇔ \(\left[{}\begin{matrix}cos\left(3x\right)=-1\\cos\left(3x\right)=1\end{matrix}\right.\)⇔\(\left[{}\begin{matrix}x=\dfrac{\pi}{3}+\dfrac{k2\pi}{3}\\x=\dfrac{k2\pi}{3}\end{matrix}\right.\)