K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MN
6 tháng 7 2021
Bài 3:
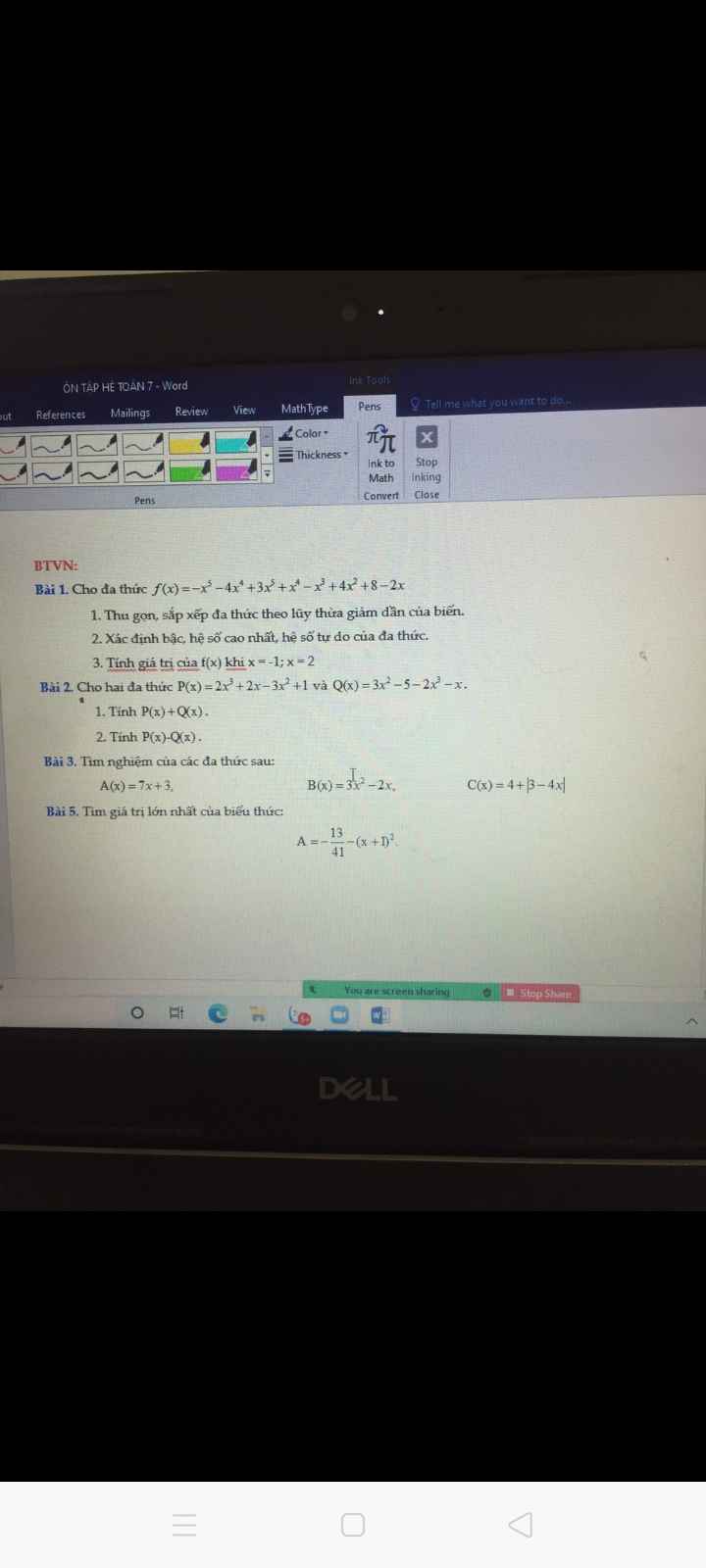
a) Cho A(x)=0 hay 7x+3=0
Ta có 7x+3=0 => 7x=3 => x=\(\dfrac{3}{7}\)
Vậy nghiệm của đa thức A(x) là \(\dfrac{3}{7}\)
16 tháng 7 2021
a) Ta có: \(\widehat{MPD}=\dfrac{\widehat{MPN}}{2}\)(PD là tia phân giác của \(\widehat{MPN}\))
\(\widehat{MNA}=\dfrac{\widehat{MNP}}{2}\)(NA là tia phân giác của \(\widehat{MNP}\))
mà \(\widehat{MPN}=\widehat{MNP}\)(ΔMNP vuông cân tại M)
nên \(\widehat{MPD}=\widehat{MNA}\)
Xét ΔMNA vuông tại M và ΔMPD vuông tại M có
MN=MP(ΔMNP vuông cân tại M)
\(\widehat{MPD}=\widehat{MNA}\)(cmt)
Do đó: ΔMNA=ΔMPD(Cạnh góc vuông-góc nhọn kề)
Suy ra: MA=MD(Hai cạnh tương ứng)
hay DN=AP(đpcm)
VN
11 tháng 1 2023
a)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{x+y+z}{3+5+6}=\dfrac{98}{14}=7\)
\(+)\)\(\dfrac{x}{3}=7\Rightarrow x=7\times3=21\)
\(+)\)\(\dfrac{y}{5}=7\Rightarrow y=7\times5=35\)
\(+)\)\(\dfrac{z}{6}=7\Rightarrow z=7\times6=42\)
Vậy \(x=21;y=35;z=42\)
b)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{2}=\dfrac{x+y-z}{4+5-2}=\dfrac{21}{7}=3\)
\(+)\)\(\dfrac{x}{4}=3\Rightarrow x=3\times4=12\)
\(+)\)\(\dfrac{y}{5}=3\Rightarrow y=3\times5=15\)
\(+)\)\(\dfrac{z}{2}=3\Rightarrow z=3\times2=6\)
Vậy \(x=12;y=15;z=6\)
c)
Ta có :
\(x:y:z=5:\left(-6\right):7\) và \(x-y-z=16\)
\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{-6}=\dfrac{z}{7}\) và \(x-y-z=16\)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{5}=\dfrac{y}{-6}=\dfrac{z}{7}=\dfrac{x-y-z}{5-\left(-6\right)-7}=\dfrac{16}{4}=4\)
\(+)\)\(\dfrac{x}{5}=4\Rightarrow x=4\times5=20\)
\(+)\)\(\dfrac{y}{-6}=4\Rightarrow y=4\times\left(-6\right)=-24\)
\(+)\)\(\dfrac{z}{7}=4\Rightarrow z=4\times7=28\)
Vậy \(x=20;y=-24;z=28\)
d)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+z}{2+4}=\dfrac{18}{6}=3\)
\(+)\)\(\dfrac{x}{2}=3\Rightarrow x=3\times2=6\)
\(+)\)\(\dfrac{y}{3}=3\Rightarrow y=3\times3=9\)
\(+)\)\(\dfrac{z}{4}=3\Rightarrow z=3\times4=12\)
Vậy \(x=6;y=9;z=12\)
e)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{7}=\dfrac{x-y}{5-6}=\dfrac{36}{-1}=-36\)
\(+)\)\(\dfrac{x}{5}=-36\Rightarrow x=-36\times5=-180\)
\(+)\)\(\dfrac{y}{6}=-36\Rightarrow y=-36\times6=-216\)
\(+)\)\(\dfrac{z}{7}=-36\Rightarrow z=-36\times7=-252\)
Vậy \(x=-180;y=-216;z=-252\)
11 tháng 1 2023
a: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{x+y+z}{3+5+6}=\dfrac{98}{14}=7\)
=>x=21; y=35; z=42
b: x/4=y/5=z/2 và x+y-z=21
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{2}=\dfrac{x+y-z}{4+5-2}=\dfrac{21}{7}=3\)
=>x=12; y=15; z=6
c: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{5}=\dfrac{y}{-6}=\dfrac{z}{7}=\dfrac{x-y-z}{5+6-7}=\dfrac{16}{4}=4\)
=>x=20; y=-24; z=28
d: Áp dụng tính chất của DTSBN, ta được:
x/2=y/3=z/4=(x+z)/(2+4)=18/6=3
=>x=6; y=9; z=12
TN
0
4 tháng 9 2021
Gọi chiều dài là x, chiều rộng là y
=> Ta có: \(\dfrac{x}{3}=\dfrac{y}{2}\) và xy = 150 (m2)
Đặt \(\dfrac{x}{3}=\dfrac{y}{2}\) = k.
=> x = 3k và y = 2k
=> 3k . 2k = 6k^2
⇔ 6k^2 = 150 (m2)
⇔ k^2 = 150 : 6
⇔ k^2 = 25
⇔ \(5^2=25\)
=> x = 15 ; y = 10
Vậy chiều dài = 15 (m) ; chiều rộng = 10 (m)
Chu vi của khu đất hình chữ nhật là:
(15+10) . 2 = 50 (m)
H
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
S
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
21 tháng 5 2021
a)xét ΔBEA và ΔBEC có:
\(\widehat{BEC}=\widehat{BEA}=90^o\)
AB=BC(ΔABC cân tại B)
\(\widehat{BCE}=\widehat{BAE}\)(ΔABC cân tại B)
⇒ΔBEA=ΔBEC (c.huyền.g.nhọn)
b)vì ΔBEA=ΔBEC nên AE=CE(2 cạnh tương ứng)
⇒E là trung điểm của AC
⇒BE là đường trung tuyến của ΔABC (đ.p.ch/m)(1)
c) Ta có:
vì D là trung điểm của BC⇒AD là đường trung tuyến của ΔABC(2)
từ (1)và(2) ⇒K là trọng tâm của ΔABC
⇒KD=\(\dfrac{1}{2}KA\)
xét ΔABK có:
KB+KA>AB(bất đẳng thức tam giác)
hay KB+2KD>AB
mà AB=BC
⇒KB+2KD>BC(đ.p.ch/m)
TT
13 tháng 11 2014
=> x-3x = -3 + 1
=> x (1-3) = -2
=> -2x = -2
=> x = -2 : (-2)
=> x = 1
6 tháng 3 2015
x +3 = 3x +1
=> 3x - x = 3 - 1
=> 2x = 2
=> x = 1
Vậy: x = 1
(đây là cách nhanh nhất, like giùm mình nha!)
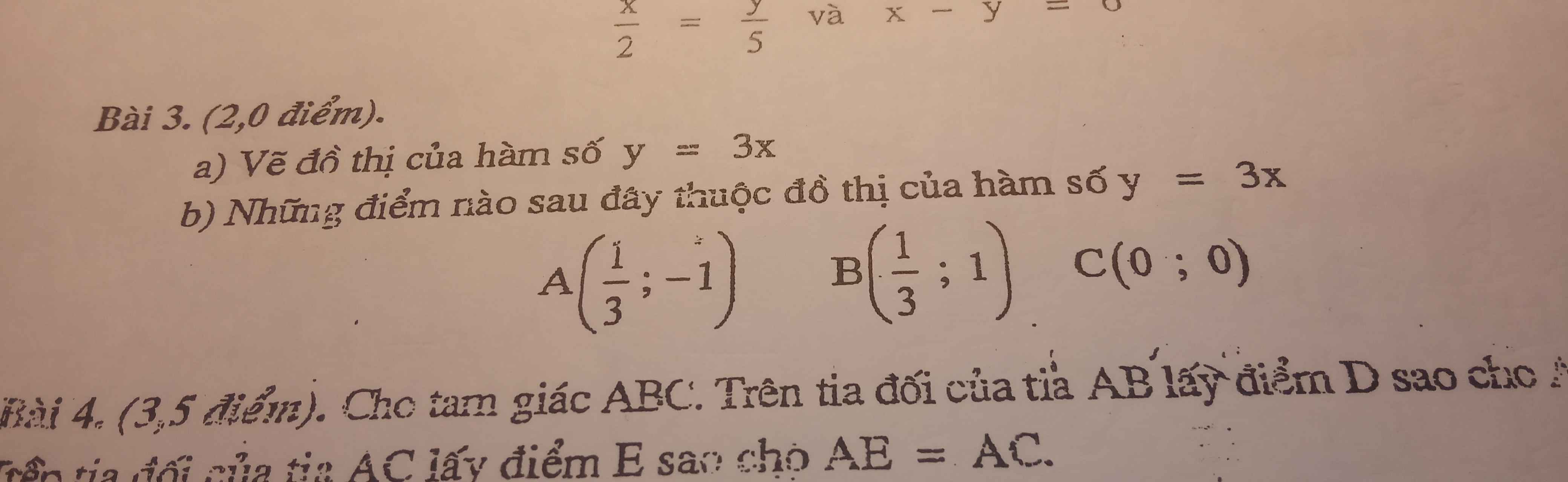
Cả bài 4 nữa nhé