
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)
\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)
\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)
\(\Rightarrow\) vô nghiệm.

\(\left\{{}\begin{matrix}6u_2+u_5=1\\3u_3+2u_4=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6u_1.q+u_1.q^4=1\\3u_1.q^2+2u_1.q^3=-1\end{matrix}\right.\)
\(\Rightarrow u_1\left(6q+q^4+3q^2+2q^3\right)=0\)
\(\Leftrightarrow q^3+2q^2+3q+6=0\)
\(\Leftrightarrow\left(q+2\right)\left(q^2+3\right)=0\)
\(\Leftrightarrow q=-\text{}2\)
\(\Rightarrow u_1=\dfrac{1}{4}\)
\(\Rightarrow u_n=u_1.q^{n-1}=\dfrac{1}{4}.\left(-2\right)^{n-1}=\left(-2\right)^{n-3}\)

a, \(u_n=u_1.q^{n-1}\)
\(\Leftrightarrow192=u_1.2^n\)
\(\Leftrightarrow u_1=\dfrac{192}{2^n}\)
\(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}\)
\(\Leftrightarrow189=\dfrac{\dfrac{192}{2^n}\left(1-2^n\right)}{1-2}\)
\(\Leftrightarrow189=192-\dfrac{192}{2^n}\)
\(\Leftrightarrow\dfrac{192}{2^n}=3\)
\(\Leftrightarrow2^n=2^6\)
\(\Rightarrow n=6\)


Do MN là đường trung bình tam giác ABC \(\Rightarrow MN||AB\) mà \(AB||CD\Rightarrow MN||CD\)
MN và (ABCD) không có điểm chung \(\Rightarrow MN||\left(ABCD\right)\)
MN và (SCD) không có điểm chung \(\Rightarrow MN||\left(SCD\right)\)
MN nằm trên (SAB) nên MN không song song (SAB)
Vậy MN song song với cả (ABCD) và (SCD)

a: AD vuông góc CD
SA vuông góc CD
=>CD vuông góc (SAD)
Kẻ AH vuông góc SD
=>CD vuông góc AH
mà SD vuông góc AH
nên AH vuông góc (CDS)
=>d(A;(SCD))=AH=căn (4a^2+16a^2/8a^2)=căn 10/2
Kẻ MP//AB//CD
=>AP/AD=AM/AC
=>AP/4a=1/4
=>AP=a
=>PD=3a
PQ vuông góc SD
PQ vuông góc CD
=>PQ vuông góc (SCD)
mà PM//(SCD)
nên d(P;(SCD))=PQ
Xét ΔADH có PQ/AH=PD/AD
\(\dfrac{PQ}{\sqrt{10}:2}=\dfrac{3a}{4a}=\dfrac{3}{4}\)
=>PQ=3 căn 10/8
=>d(M;(SCD))=PQ=3căn 10/8
Kẻ NG//AM
Kẻ GU vuông góc SD
=>d(G;(SCD))=GU
GU/AH=SG/SA=1/2
=>GU=căn 10/4
b: (SCD;ABCD))=(AD;SD)=góc ADH
AH=AD*cosADH
=>cosADH=căn 10/8
=>góc ADH=67 độ
(SBD;(ABCD))=góc SOA
SA=AO*tan SOA
=>tan SOA=2/5
=>góc SOA=22 độ

A là khẳng định sai
Lăng trụ có đáy là đa giác đều chưa chắc là 1 lăng trụ đều
Để 1 lăng trụ là đều thì nó cần 2 yếu tố: đó là lăng trụ đứng, và đáy là đa giác đều

a: \(N\in SB\subset\left(SBC\right)\)
\(N\in\left(NAD\right)\)
Do đó: \(N\in\left(SBC\right)\cap\left(NAD\right)\)
Xét (SBC) và (NAD) có
\(N\in\left(SBC\right)\cap\left(NAD\right)\)
BC//AD
Do đó: (SBC) giao (NAD)=xy, xy đi qua N và xy//BC//AD
b: Trong mp(ABCD), Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\left(1\right)\)
\(S\in SA\subset\left(SAC\right)\)
\(S\in SB\subset\left(SBD\right)\)
Do đó: \(S\in\left(SAC\right)\cap\left(SBD\right)\left(2\right)\)
Từ (1) và (2) suy ra (SAC) giao (SBD)=SO
c: Chọn mp(SBC) có chứa NK
\(SC\subset\left(SBC\right)\)
\(SC\subset\left(SCA\right)\)
Do đó: \(\left(SBC\right)\cap\left(SCA\right)=SC\)
Gọi E là giao điểm của NK với SC
=>E là giao điểm của NK với mp(SAC)
d: Chọn mp(SBD) có chứa DN
Ta có: (SBD) giao (SAC)=SO(cmt)
nên ta sẽ gọi F là giao điểm của SO với DN
=>F là giao điểm của ND với mp(SAC)
e: Xét ΔSAB có
M,N lần lượt là trung điểm của SA,SB
=>MN là đường trung bình của ΔSAB
=>MN//AB và \(MN=\dfrac{AB}{2}\)
MN//AB
AB//CD
Do đó: MN//CD
Xét tứ giác MNCD có MN//CD
nên MNCD là hình thang









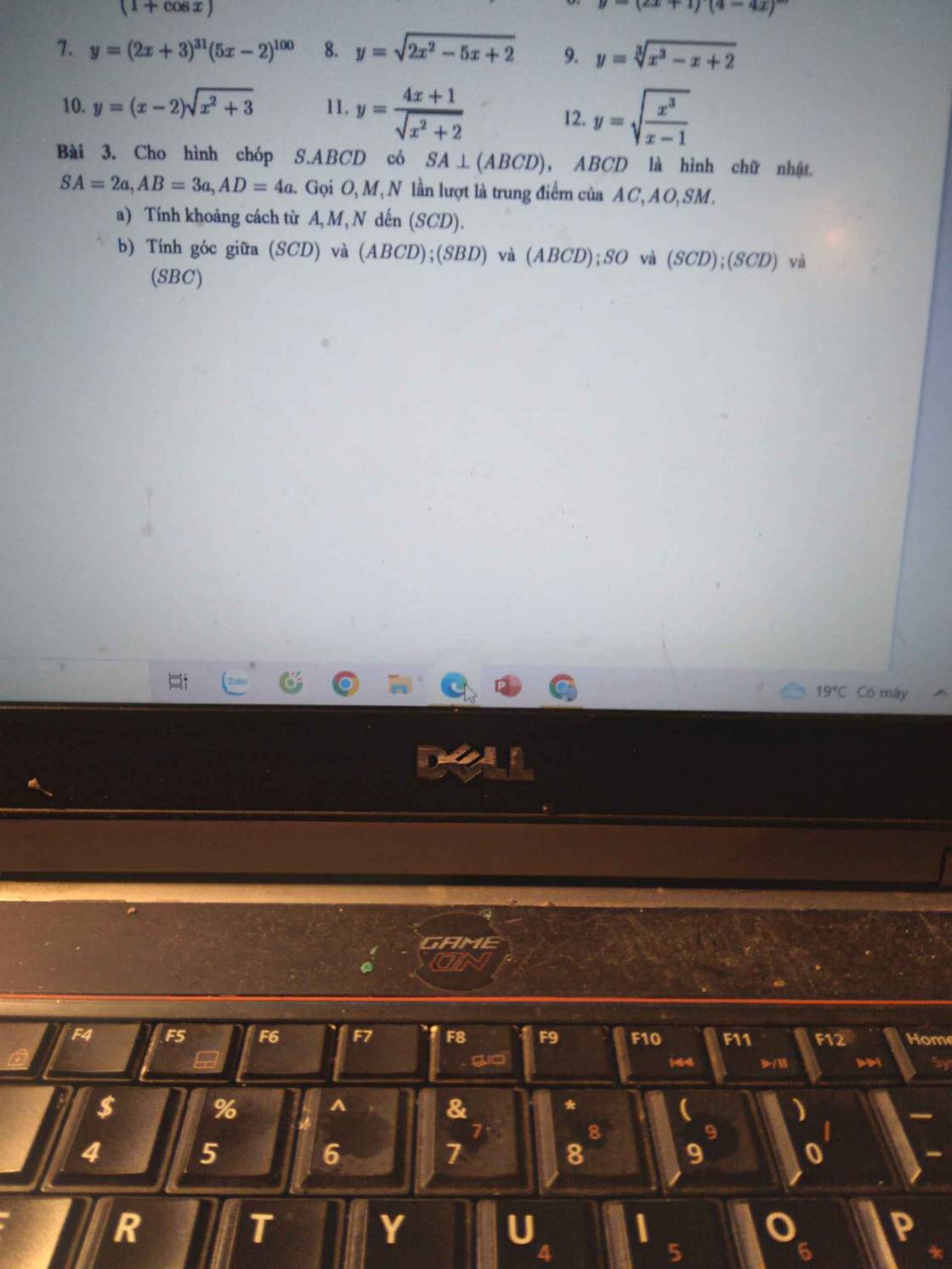 Giúp em bài 3 với ạ. Em cảm ơn ạ
Giúp em bài 3 với ạ. Em cảm ơn ạ

NO
Từ giả thiết 1 và 3 có: \(\left\{{}\begin{matrix}y^2=xz\left(1\right)\\x+y+z=13\left(2\right)\end{matrix}\right.\)
Từ giả thiết 2: \(\left\{{}\begin{matrix}x=u_0\\y=u_0+2d\\z=u_0+8d\end{matrix}\right.\) \(\left(3\right)\)
Thế hệ (3) vào hai phương trình (1) và (2) có:
\(\left\{{}\begin{matrix}\left(u_0+2d\right)^2=u_0\left(u_0+8d\right)\\3u_0+10d=13\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}4u_0d-4d^2=0\\3u_0+10d=13\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}d=0,u_0=\dfrac{13}{3}\\d=u_0=1\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=y=z=\dfrac{13}{3}\\x=1,y=3,z=9\end{matrix}\right.\)