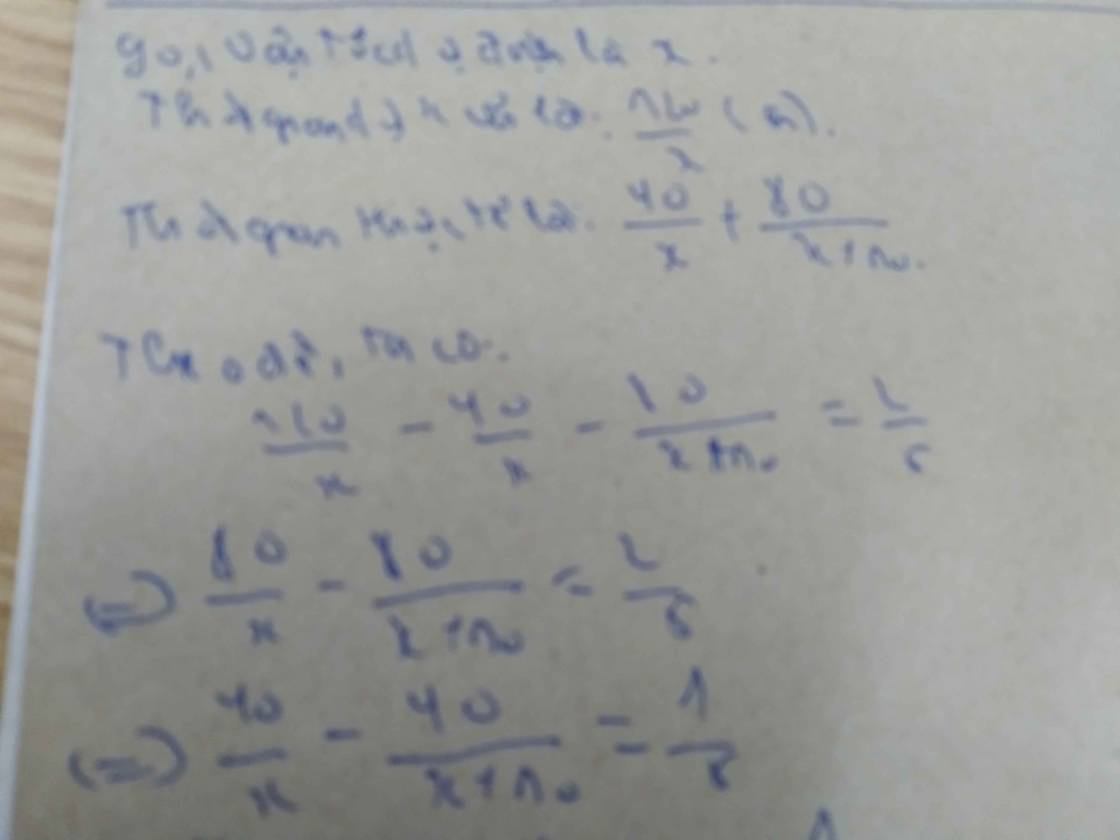Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi vận tốc dự định của xe là x (x>0)
vận tốc xe khi đi được \(\dfrac{1}{3}\)quãng đường là x+10
đổi 20'=\(\dfrac{1}{3}\)h -
theo bài ra ta có pt:\(\dfrac{40}{x}\)+\(\dfrac{20}{x+10}\)-\(\dfrac{60}{x}\)=\(\dfrac{1}{3}\)
=>\(x^2\) +10x=1200
=>\(x^2\)+10x -1200=0(a=1, b'=5, c= -1200)
ta có \(\Delta'\)=\(b^2\)-ac = \(5^2\)-(-1200) = 25 +1200 = 1225>0
=>\(\sqrt{1225}\)= 35
pt có 2 nghiệm phân biệt
x1 = \(\dfrac{-5+35}{1}\)= 30(TM)
x2=\(\dfrac{-5-35}{1}\)=-40(Ko TM)
vậy vận tốc ban đầu là 30km/h
thời gian đi là 2h20'
Vậy vận tốc dự định của người đó la 40 km/h.
Thời gian người đó đi từ A đến B là 2040+4040−10=1164020+40−1040=611 (giờ) = 1 giờ 50 phút

Gọi độ dài quãng đường \(AB\) là: \(a\left(km\right)\left(a>0\right)\)
Gọi thời gian dự định ban đầu là:\(b\left(h\right)\left(b>0\right)\)
Ta có: \(10b=a\)
\(\Rightarrow10b-a=0\)
Người đó đi được nửa đường thì hết số thời gian:
\(\frac{0,5a}{10}=0,05a\)
Còn lại số thời gian:
\(b-0,05a-0,5\)
\(\Rightarrow15\left(b-0,05a-0,5\right)=0,5a\)
\(\Rightarrow15b-1,25a=7,5\)
Từ đó ta có hệ phương trình sau:
\(10b-a=0\)
\(\Leftrightarrow15b-1,25a=7,5\)\(\Leftrightarrow\hept{\begin{cases}a=30\\b=3\end{cases}}\)
Vậy \(s_{AB}=30km\)

Giải:
Quãng đường còn lại người đó phải đi là:
150 \(\times\) (1 - \(\dfrac{1}{5}\)) = 120 (km/h)
Gọi vận tốc dự định là \(x\)(km/h) ; \(x\) > 0
Vận tốc thực tế là: \(x\) + 10 (km/h)
Thời gian người đó đi hết quãng đường còn lại với vận tốc dự định là:
120 : \(x\) = \(\dfrac{120}{x}\) (giờ)
Thời gian người đó đi hết quãng đường còn lại với vận tốc thực tế là:
120 : (\(x\) + 10) = \(\dfrac{120}{x+10}\) (giờ)
Đổi 36 phút = \(\dfrac{3}{5}\) giờ
Theo bài ra ta có phương trình:
\(\dfrac{120}{x}\) - \(\dfrac{120}{x+10}\) = \(\dfrac{3}{5}\)
120.(\(\dfrac{1}{x}\) - \(\dfrac{1}{x+10}\)) = \(\dfrac{3}{5}\)
120. \(\dfrac{x+10-x}{x\left(x+10\right)}\)= \(\dfrac{3}{5}\)
120.\(\dfrac{\left(x-x\right)+10}{x\left(x+10\right)}\) = \(\dfrac{3}{5}\)
\(\dfrac{120.10}{x\left(x+10\right)}\) = \(\dfrac{3}{5}\)
\(x\)(\(x\) + 10) = 120.10 : \(\dfrac{3}{5}\)
\(x\)(\(x+10\)) = 2000
\(x^2\) + 10\(x\) - 2000 = 0
\(\Delta\)' = 52 + 2000 = 2025 > Vậy phương trình có hai nghiệm phân biệt là
\(x_1\) = \(\dfrac{-5+\sqrt{2025}}{1}\) = 40 > 0(tm)
\(x_2\) = \(\dfrac{-5-\sqrt{2025}}{1}\) = - 50 < 0 (loại)
Vậy vận tốc ban đầu của người đó là 40 km/h
Thời gian thực tế người đó đi hết quãng đường AB là:
150 : 40 - \(\dfrac{3}{5}\) = 3,15 (giờ)
3,15 giờ = 3 giờ 9 phút
Kết luận: Vận tốc dự định của người đó là 40 km/h
Thời gian thực tế người đó đi hết quãng đường từ A đến B là 3 giờ 9 phút.

Gọi vận tốc dự định là x
Vận tốc đi trên S còn lại là : x+10 Dk :x>0
Vì người đó đến B sớm hơn dự định 24phut (=0,4h) nên ta có pt :
40/x +80/x+10 +0,4 = 120/x
0,4 = 80/x - 80/x+10
0,4=800/x(x+10)
x2+10x=2000
x2+10x-2000=0
(x-40)(x+50)=0
Vi x>0 => x+50>0
=> x-40 =0
x=40(km/h)