
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

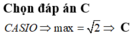

Đáp án: A.
Ta có y(0) = -5, y(3) = -2, tọa độ đỉnh: x = -b/2a = 2
⇒ y(2) = -4 + 8 - 5 = -1; max y = max(-5; -2; -1) = -1.
Cách khác: Vì a = -1 nên parabol y = -x2 + 4x - 5 đạt cực đại tại đỉnh (2; -1). Vì vậy GTLN của hàm số trên đoạn [0;3] là y(2) = -1

Đáp án: A.
Ta có y(0) = -5, y(3) = -2, tọa độ đỉnh: x = -b/2a = 2
⇒ y(2) = -4 + 8 - 5 = -1; max y = max(-5; -2; -1) = -1.
Cách khác: Vì a = -1 nên parabol y = - x 2 + 4x - 5 đạt cực đạt tại đỉnh (2; -1). Vì vậy giá trị lớn nhất của hàm số trên đoạn [0;3] là y(2) = -1.

Đáp án: A.
Tập xác định: D = R \{3}
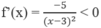 ∀x ∈ D.
∀x ∈ D.
Do đó f(x) nghịch biến trên (- ∞ ; 3) và (3; + ∞ ).
Ta thấy [0;2] ⊂ (- ∞ ;3). Vì vậy
max f(x) = f(0) = 1/3, min f(x) = f(2) = -3.

Chọn C
Tập xác định của hàm số là ℝ .
Ta có: ![]()
Vì trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1 nên hàm số đạt cực trị tại x = -1( cũng là điểm cực đại của hàm số) và a > 0.
![]()
![]()
![]()
Khi đó f'(x) = 0 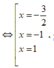 ( đều là các nghiệm đơn)
( đều là các nghiệm đơn)
Hàm số đạt cực đại tại x = -1 nên có bảng biến thiên:
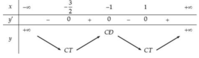
=> x = - 3 2 là điểm cực tiểu duy nhất thuộc - 2 ; - 5 4
Vậy hàm số đạt giá trị nhỏ nhất tại x = - 3 2 trên đoạn - 2 ; - 5 4

a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:

Vì

nên ta có đồ thị f(x) như sau:

Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,

Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2

Đáp án: A.
Tập xác định: D = R \{3}
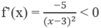 ∀
x
∈
D.
∀
x
∈
D.
Do đó f(x) nghịch biến trên (- ∞ ; 3) và (3; + ∞ ).
Ta thấy [0;2] ⊂ (- ∞ ;3). Vì vậy
max f(x) = f(0) = 1/3, min f(x) = f(2) = -3.

\(y'=\dfrac{3}{\left(x+2\right)^2}>0\Rightarrow\) hàm đồng biến trên đoạn đã cho
\(\Rightarrow\max\limits_{\left[0;1\right]}y=y\left(1\right)=0\)

Chọn B
Vì y = a x 3 + c x + d , a ≠ 0 là hàm số bậc ba và có m i n x ∈ - ∞ ; 0 f ( x ) = f ( - 2 ) nên a < 0 và y' = 0 có hai nghiệm phân biệt.
Ta có ![]() có hai nghiệm phân biệt
⇔
ac < 0
có hai nghiệm phân biệt
⇔
ac < 0
Vậy với a < 0, c > 0 thì y' = 0 có hai nghiệm đối nhau 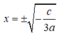
Từ đó suy ra
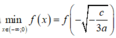
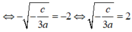
⇔
c = -12a
Ta có bảng biến thiên
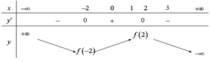
Ta suy ra ![]()

Giá trị nhỏ nhất của hàm số trên đoạn [-2,3] là điểm thấp nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị nhỏ nhất tại x = -2. Thay x = -2 vào hàm số y đã cho ta có giá trị nhỏ nhất là -2.
Giá trị lớn nhất của hàm số trên đoạn [-2,3] là điểm cao nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị lớn nhất tại x = 3. Thay x = 3 vào hàm số y đã cho ta có giá trị lớn nhất là 3.