
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 4a.
Kẻ tia $Om\parallel Ax$ như hình:
Vì $Ax\parallel Om$ nên $\widehat{AOm}=\widehat{xAO}=30^0$ (hai góc so le trong)
$\Rightarrow \widehat{mOB}=\widehat{AOB}-\widehat{AOm}=70^0-30^0=40^0$
$Ax\parallel By, Ax\parallel Om\Rightarrow By\parallel Om$
$\Rightarrow \widehat{B}=\widehat{mOB}=40^0$ (hai góc so le trong)
a) Trên nửa mặt phẳng bờ OB chứa điểm A, kẻ tia Oz//Ax//By
Ta có: Oz//Ax(cách vẽ)
\(\Rightarrow\widehat{xAO}=\widehat{AOz}=30^0\)( 2 góc so le trong)
Ta có: \(\widehat{AOz}+\widehat{zOB}=\widehat{AOB}\)
\(\Rightarrow\widehat{zOB}=\widehat{AOB}-\widehat{AOz}=70^0-30^0=40^0\)
Ta có: Oz//By
\(\Rightarrow\widehat{B}=\widehat{zOB}=40^0\)( 2 góc so le trong)
b) Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)( tổng 3 góc trong tam giác)
\(\Rightarrow\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-60^0-40^0=80^0\)
\(\Rightarrow y=80^0\)
Xét tứ giác AEDB có:
\(\widehat{AED}+\widehat{EDB}+\widehat{ABD}+\widehat{BAE}=360^0\)
\(\Rightarrow\widehat{EDB}=360^0-\widehat{AED}-\widehat{ABD}-\widehat{BAE}=360^0-90^0-40^0-60^0=170^0\)
\(\Rightarrow x=170^0\)


Tam giác AHC vuông tại H ( do AH \(⊥\)BC )
=> AH2 + CH2 = AC2 ( định lý Pytago )
=> 42 + CH2 = 52
=> 9 + CH2 = 25
=> CH2 = 16
=> CH = 4 cm ( CH > 0 )
Ta có: CH + BH = BC
=> 4 + BH = 9
=> BH = 5 cm
Tam giác AHC vuông tại H ( do AH\(⊥\)BC )
=> AH2 + CH2 = AC2 ( định lý Pytago )
=> 42 + CH2 = 52
=> 16 + CH2 = 25
=> CH2 = 9
=> CH = 3 cm ( CH > 0 )
Ta có: CH + BH = BC
=> 3 + BH = 9
=> BH = 6 cm
Tam giác ABH vuông tại H ( do AH\(⊥\)BC )
=> AH2 + BH2 = AB2 ( định lý Pytago )
=> 42 + 62 = AB2
=> 16 + 36 = AB2
=> AB2 = 52
=> AB = \(\sqrt{52}\)cm ( AB > 0 )
Xin lỗi bạn nhé, bài trên mình chưa để ý đề bài và làm sai, mình làm lại bài này, bạn vẫn dùng hình ở trên nha!
=> AB2 =

Bài 6
a) (3x² + 5) + [(2x² - 5x) - (5x² + 4)]
= 3x² + 5 + (2x² - 5x - 5x² - 4)
= 3x² + 5 + 2x² - 5x - 5x² - 4
= (3x² + 2x² - 5x²) - 5x + (5 - 4)
= -5x + 1
---------‐----------
b) (x + 2)(x² - 2x + 4)
= x.x² - x.2x + x.4 + 2.x² - 2.2x + 2.4
= x³ - 2x² + 4x + 2x² - 4x + 8
= x³ + (-2x² + 2x²) + (4x - 4x) + 8
= x³ + 8
-------------------
c) (4x³ - 8x² + 13x - 5) : (2x - 1)
= (4x³ - 2x² - 6x² + 3x + 10x - 5) : (2x - 1)
= [(4x³ - 2x²) - (6x² - 3x) + (10x - 5)] : (2x - 1)
= [2x²(2x - 1) - 3x(2x - 1) + 5(2x - 1)] : (2x - 1)
= (2x - 1)(2x² - 3x + 5) : (2x - 1)
= 2x² - 3x + 5

các bạn ơi mình đg cần rất gấp mong các bạn có thể giúp mình liền ạ. cảm on các bạn nhiều.
a) Xét ΔAFC vuông tại F có \(\widehat{A}=45^0\)(gt)
nên ΔAFC vuông cân tại F(Dấu hiệu nhận biết tam giác vuông cân)
hay FA=FC(Hai cạnh bên)(đpcm)
 Gi ải giúp mình vs ah
Gi ải giúp mình vs ah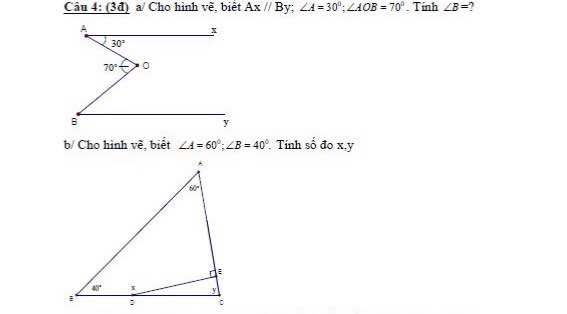
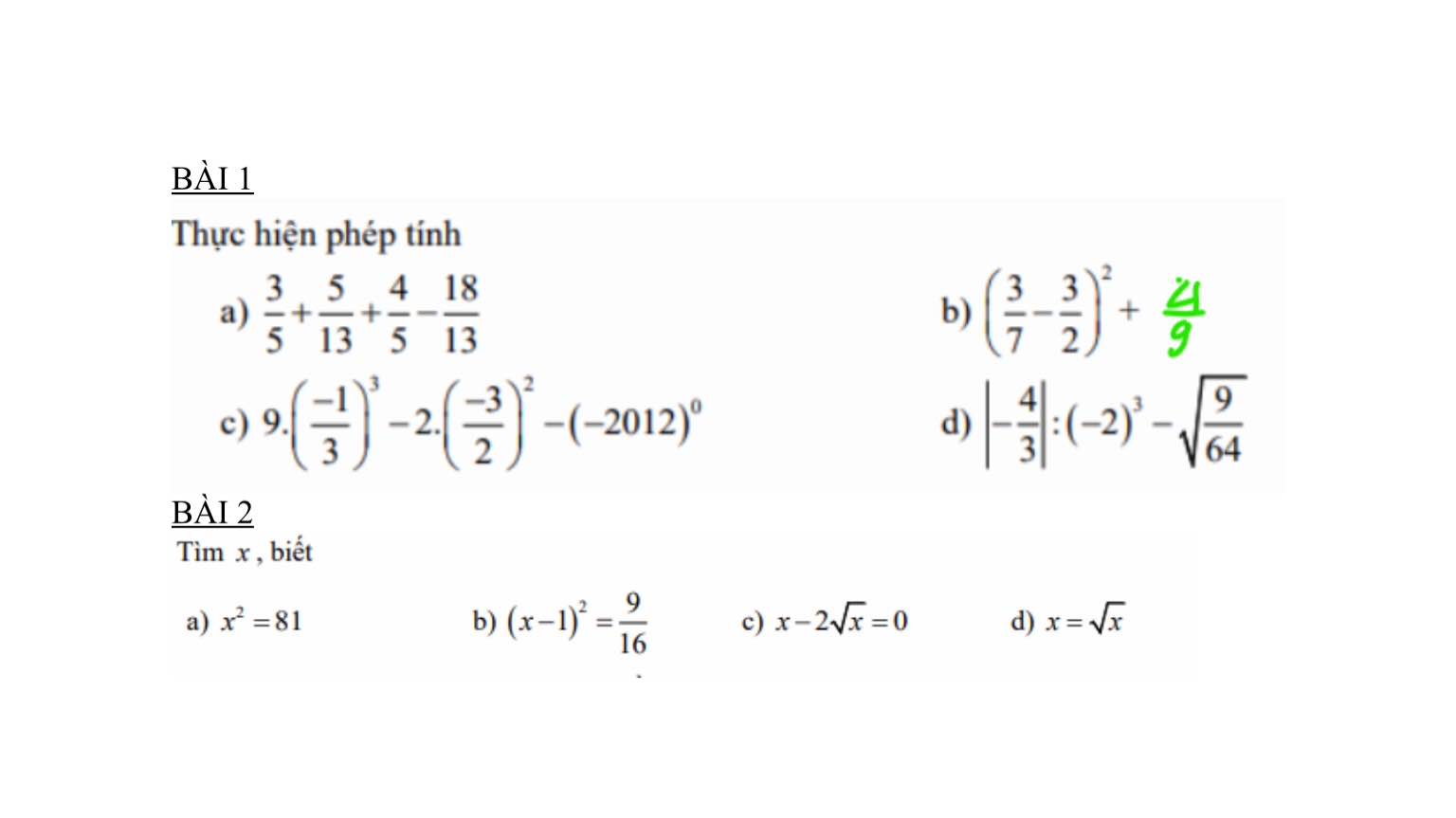 Mn lm giúp mình vs ah mình cần gấp !!!
Mn lm giúp mình vs ah mình cần gấp !!! Gi ải hộ bài 2
Gi ải hộ bài 2 
a: \(M\left(x\right)=3x^2+x^2+4x^4-x-3x^3+5x^4+x^2-6\)
\(=\left(4x^4+5x^4\right)-3x^3+\left(3x^2+x^2+x^2\right)-x-6\)
\(=9x^4-3x^3+5x^2-x-6\)
\(N\left(x\right)=-x^2-x^4+4x^3-x^2-5x^3+3x+1+x\)
\(=-x^4+\left(4x^3-5x^3\right)+\left(-x^2-x^2\right)+4x+1\)
\(=-x^4-x^3-2x^2+4x+1\)
b: M(x)+N(x)
\(=9x^4-3x^3+5x^2-x-6-x^4-x^3-2x^2+4x+1\)
\(=8x^4-4x^3+3x^2+3x-5\)
M(x)-N(x)
\(=9x^4-3x^3+5x^2-x-6+x^4+x^3+2x^2-4x-1\)
\(=10x^4-2x^3+7x^2-5x-7\)
c: P(x)=M(x)-N(x)
\(=10x^4-2x^3+7x^2-5x-7\)
bậc là 4
hệ số cao nhất là 10
Hệ số tự do là -7
d: \(P\left(-2\right)=10\cdot\left(-2\right)^4-2\cdot\left(-2\right)^3+7\cdot\left(-2\right)^2-5\cdot\left(-2\right)-7\)
\(=10\cdot16+2\cdot8+7\cdot4+10-7\)
=160+16+28+3
=176+31
=207