Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dung à mày (:
Ta có \(\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{a}{x+1}+\frac{b}{\left(x+1\right)^2}+\frac{c}{x+2}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{a\left(x+1\right)\left(x+2\right)}{\left(x+1\right)^2\left(x+2\right)}+\frac{b\left(x+2\right)}{\left(x+1\right)^2\left(x+2\right)}+\frac{c\left(x+1\right)^2}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{a\left(x^2+3x+2\right)}{\left(x+1\right)^2\left(x+2\right)}+\frac{bx+2b}{\left(x+1\right)^2\left(x+2\right)}+\frac{c\left(x^2+2x+1\right)}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{ax^2+3ax+2a+bx+2b+cx^2+2cx+c}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Leftrightarrow\frac{1}{\left(x+1\right)^2\left(x+2\right)}=\frac{x^2\left(a+c\right)+x\left(3a+b+2c\right)+\left(2a+2b+c\right)}{\left(x+1\right)^2\left(x+2\right)}\)
\(\Rightarrow1=x^2\left(a+c\right)+x\left(3a+b+2c\right)+\left(2a+2b+c\right)\)
Đồng nhất hệ số ta được :
\(\hept{\begin{cases}a+c=0\\3a+b+2c=0\\2a+2b+c=1\end{cases}}\)=> Chịu :)) Khó quá không làm được ... Hoặc do đề sai ;-;
Không sai == Trong sách Nâng cao và phát triển toán 8 tập 1 trang 33 bài 123 ý c
T cũng chịu '-'


Mẹo thì không có đâu bạn ạ! ^_^. Cơ bản là bạn phải hiểu vấn đề của bài thôi!
Bạn thử lên youtube học của THẦY QUANG thử xem
Thầy này dạy dễ hiểu lắm

-Đặt \(x^2+y^2=a;z^2-x^2=b;-y^2-z^2=c\Rightarrow a+b+c=0\)
-Ta c/m: \(a^3+b^3+c^3=3abc\) thì sẽ ra như đề bài.
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\) (luôn đúng)

xét tam giác ABC có
BD là tia phân giác góc B(gt)
=> \(\dfrac{BA}{BC}=\dfrac{DA}{DC}\) (tính chất đường phân giác)
=> \(\dfrac{DA}{DC}=\dfrac{6}{10}=>\dfrac{DA}{DC}=\dfrac{3}{5}=>\dfrac{DA}{3}=\dfrac{DC}{5}\)
mà AC=6cm
áp dụng dãy tỉ số bằng nhau ta có
\(\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{6}{8}=0,75\left(cm\right)\)
=> DA=0,75*3=2,25(cm)
c/m tương tự ta có EA=2,25(cm)
có \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\left(\dfrac{2,25}{6}=\dfrac{2,25}{6}\right)\)
=> ED//BC ( ta lét đảo)
=> \(\dfrac{AE}{AB}=\dfrac{ED}{BC}=>\dfrac{2,25}{6}=\dfrac{ED}{10}=>ED=3,75\left(cm\right)\)

a
Xét tam giác AEM và tam giác CBM có:
\(AM=MC\)
\(ME=MB\)
\(\Rightarrow\Delta AEM=\Delta CBM\left(2cgv\right)\)
\(\Rightarrow\widehat{EAM}=\widehat{ECB}\)
Mà \(\widehat{ECM}+\widehat{MBC}=90^0\Rightarrow\widehat{EAM}+\widehat{MBC}=90^0\Rightarrowđpcm\)
b
Gọi O là giao điểm của DM và AC
Xét tam giác CAK vuông tại A có KO là đường trung tuyến ứng với cạnh huyền
\(\Rightarrow KO=\frac{1}{2}AC\)
Mà \(AC=BD\Rightarrow KO=\frac{1}{2}MD\Rightarrow\Delta KMD\) vuông tại K
\(\Rightarrow\widehat{DKM}=90^0\left(1\right)\)
c
Chứng minh tương tự \(\Delta MKF\) vuông tại K
\(\Rightarrow\widehat{FKM}=90^0\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrowđpcm\)

Có rất nhiều người có trường hợp giống bạn ... mình nghĩ bạn nên xem lại các bài giảng về cách lập pt trên youtube hay gg gì đó, sau đó bạn hãy tự làm những bài tập trong SGK trước đã, không hiểu gì thì cứ đem lên đây hỏi, sẽ có người trả lời giúp bạn. Riết dần dần thì bạn cũng sẽ biết cách làm và quen với dạng này thôi. ^^
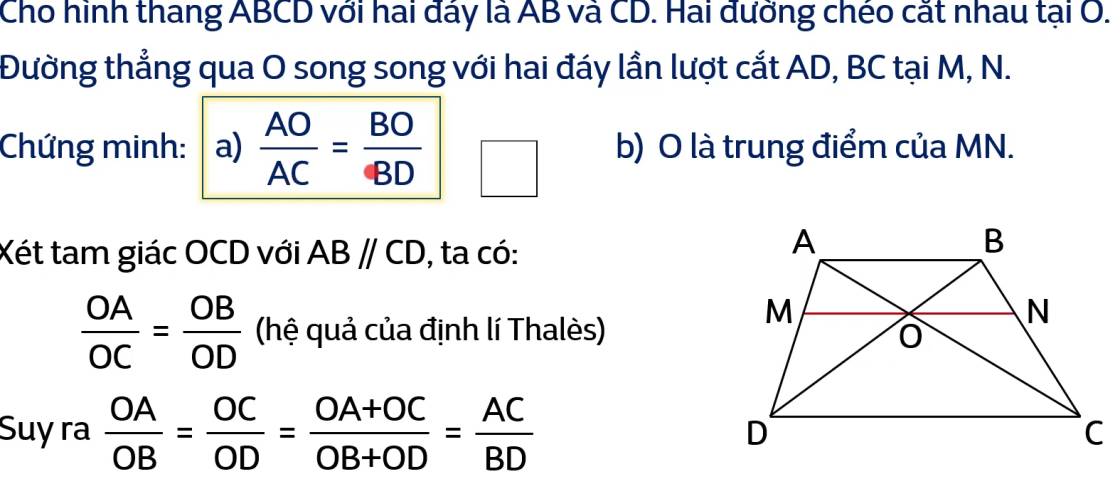
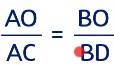
Olm chào em, vấn đề em hỏi Olm xin hỗ trợ như sau:
Đoạn \(\dfrac{OA}{OC}\) = \(\dfrac{OB}{OD}\) (hệ quả của định lí Thales). Em hiểu rồi đúng chưa.
Từ dòng suy ra \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{OA+OC}{OB+OD}\) = \(\dfrac{AC}{BD}\) là em không hiểu tại sao phải không?
Vậy Olm sẽ giảng cho em như sau:
\(\dfrac{OA}{OC}\) = \(\dfrac{OB}{OD}\) (hệ quả định lí Thales) ⇒ \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) (tc tỉ lệ thức)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{OA+OC}{OB+OD}\) (1)
Mặt khác O là giao điểm của AC và BD nên
\(\left\{{}\begin{matrix}OA+OC=AC\\OB+OD=BD\end{matrix}\right.\) (2)
Thay (2) vào (1) ta có: \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{AC}{BD}\)
Giải thích đoạn: \(\dfrac{AO}{AC}\) = \(\dfrac{BO}{BD}\)
\(\dfrac{OA}{OB}\) = \(\dfrac{AC}{BD}\) (cmt) ⇒\(\dfrac{AO}{BO}=\dfrac{AC}{BD}\) ⇒ \(\dfrac{AO}{AC}\) = \(\dfrac{BO}{BD}\) (tính chất tỉ lệ thức)
Mọi chi tiết bài giảng liên hệ zalo 0385 168 017
tại sao O lại là giao điểm của AC và BD ạ