
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từ đồ thị hàm số (C): y = f(x) ta suy ra đồ thị hàm số (C'): y = f(|x|) như sau:
+) Giữ nguyên phần đồ thị (C) trên miền x ≥ 0 , (kí hiệu phần đồ thị này là C 1 ).
+) Bỏ phần đồ thị (C) ở bên trái trục Oy.
+) Lấy đối xứng C 1 qua trục Oy, (kí hiệu phần đồ thị này là C 2 ).
Khi đó đồ thị của hàm số y = f(|x|) là hợp của hai phần đồ thị C 1 và C 2 .
Ta có đồ thị của hàm số y = f(|x|) như hình vẽ dưới đây:
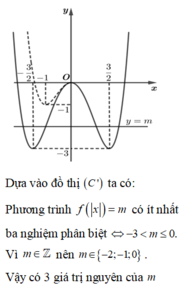
Chọn C

Lời giải:
Đặt $\sqrt{x^2+1}+x=a$ thì:
$f(a)=e^a-e^{\frac{1}{a}}$
$f'(a)=e^a+\frac{1}{a^2}.e^{\frac{1}{a}}>0$ với mọi $a$
Do đó hàm $f(a)$ là hàm đồng biến hay $f(x)$ là hàm đồng biến trên R
$\Rightarrow f(x)> f(0)=0$ với mọi $x>0$
$\Rightarrow f(\frac{12}{m+1})>0$ với $m$ nguyên dương
Do đó để $f(m-7)+f(\frac{12}{m+1})<0$ thì $f(m-7)<0$
$\Rightarrow m-7<0$
Mặt khác, dễ thấy: $f(x)+f(-x)=0$. Bây h xét:
$m=1$ thì $f(m-7)+f(\frac{12}{m+1})=f(-6)+f(6)=0$ (loại)
$m=2$ thì $f(m-7)+f(\frac{12}{m+1})=f(-5)+f(4)=f(4)-f(5)<0$ (chọn)
$m=3$ thì $f(m-7)+f(\frac{12}{m+1})=f(-4)+f(3)=f(3)-f(4)<0$ (chọn)
$m=4$ thì $f(m-7)+f(\frac{12}{m+1})=f(-3)+f(2,4)=f(2,4)-f(3)<0$ (chọn)
$m=5$ thì $f(m-7)+f(\frac{12}{m+1})=f(-2)+f(2)=0$ (loại)
$m=6$ thì $f(m-7)+f(\frac{12}{m+1})=f(-1)+f(12/7)>f(-1)+f(1)=0$ (loại)
Vậy có 3 số tm

Chọn C.
Ta có
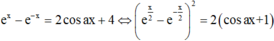
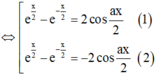
Giả sử x0 là nghiệm của phương trình ex - e-x = 2 cosax (*), thì x0 ≠ 0 và 2x0 là nghiệm của (1) và -2x0 là nghiệm của (2) hoặc ngược lại
Phương trình (*) có 5 nghiệm nên hai phương trình (1), (2) có 5 nghiệm phân biệt.
Vậy phương trình ex - e-x = 2 cosax + 4 có 10 nghiệm phân biệt.
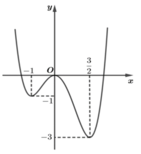

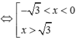
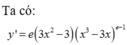

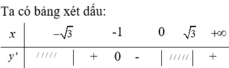


E là 1 giá trị bất kì