K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 9 2023
a) Đường thẳng \(y=3x+6\) có hệ số góc \(a=3\Rightarrow\widehat{\left(Ox;d\right)=72^o\Rightarrow góc.nhọn}\)
b) Đường thẳng \(y=-4x+1\) có hệ số góc \(a=-4\Rightarrow\widehat{\left(Ox;d\right)=-76^o\Rightarrow góc.nhọn}\)
c) Đường thẳng \(y=-3x-6\) có hệ số góc \(a=-3\Rightarrow\widehat{\left(Ox;d\right)=-71^o\Rightarrow góc.nhọn}\)
HQ
Hà Quang Minh
Giáo viên
12 tháng 9 2023
a) Đường thẳng \(y = 3x + 6\) có hệ số góc là \(a = 3 > 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là góc nhọn.
b) Đường thẳng \(y = - 4x + 1\) có hệ số góc là \(a = - 4 < 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là tù.
c) Đường thẳng \(y = - 3x - 6\) có hệ số góc là \(a = - 3 < 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là tù.
12 tháng 9 2023
a)
- Vẽ đồ thị hàm số \(y = x\).
Cho \(x = 1 \Rightarrow y = 1 \Rightarrow \)Đồ thị hàm số đi qua điểm \(M\left( {1;1} \right)\).
Đồ thị hàm số \(y = x\) là đường thẳng đi qua hai điểm \(O\) và \(M\).
- Vẽ đồ thị hàm số \(y = x + 2\)
Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(A\left( {0;2} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 2}}{1} = - 2\) ta được điểm \(B\left( { - 2;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 2\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
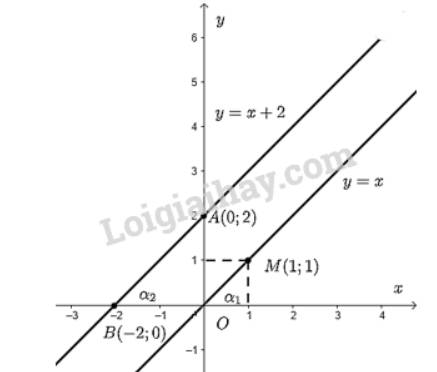
b) Góc tạo bởi hai đường thẳng \(y = x\) và \(y = x + 2\) với trục \(Ox\) lần lượt là \({\alpha _1}\) và \({\alpha _2}\).
Dùng thước đo độ kiểm tra ta thấy số đo \({\alpha _1} = {\alpha _2} = 45^\circ \).
12 tháng 9 2023
Gọi \({\alpha _1};{\alpha _2}\) lần lượt là 2 góc tạo bởi đường thẳng \({d_1};{d_2}\) với \(Ox\).
Dùng thước đo độ ta kiểm tra được\({\alpha _1} = 45^\circ ;{\alpha _2} = 135^\circ \).
HQ
Hà Quang Minh
Giáo viên
12 tháng 9 2023
b)
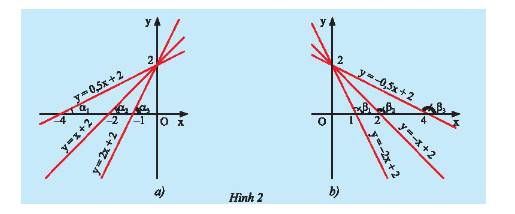
- Ở hình 2a là đồ thị của 3 hàm số \(y = 0,5x + 2;y = x + 2;y = 2x + 2\).
Ta có: \({a_1} = 0,5;{a_2} = 1;{a_3} = 2\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\alpha _1} < {\alpha _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\alpha _2} < {\alpha _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\alpha _1} < {\alpha _2} < {\alpha _3}\).
- Ở hình 2b là đồ thị của 3 hàm số \(y = - 2x + 2;y = - x + 2;y = - 0,5x + 2\).
Ta có: \({a_1} = - 2;{a_2} = - 1;{a_3} = - 0,5\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\beta _1} < {\beta _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\beta _2} < {\beta _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\beta _1} < {\beta _2} < {\beta _3}\).
HQ
Hà Quang Minh
Giáo viên
13 tháng 1
Xét (d): y = 2x+1:
Cho y = 0 thì \(x = \frac{{ - 1}}{2}\), ta được giao điểm của đồ thị với trục Ox là A(\(\frac{{ - 1}}{2};0\))
x = 0 thì y = 1, ta được giao điểm của đồ thị với trục Oy là B(0;1)
Xét (d'): y = −2x+1:
Cho y = 0 thì \(x = \frac{1}{2}\), ta được giao điểm của đồ thị với trục Ox là \(C\left( {\frac{1}{2};0} \right)\)
x = 0 thì y = 1, ta được giao điểm của đồ thị với trục Oy là B(0;1)
HQ
Hà Quang Minh
Giáo viên
9 tháng 9 2023
Khi hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là góc nhọn
Khi hệ số góc a âm thì góc tạo bởi đường thẳng này và trục Ox là góc tù.
O
0
CM
2 tháng 11 2019
- Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.
- Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm hai đáy của hình thang cân.
Đường thẳng y=x-4 có a=1>0
nên đường thẳng y=x-4 tạo với trục Ox một góc nhọn có số đo là:
\(arctan\left(1\right)=45^0\)