Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x=0
x=.................
x=-2, x=2/3
nối 2 cái xong còn cái nào bạn nối nốt nha
mình ko mang giấy bút nên ko vt đc

| CTHH của axit | tên axit | công thức gốc | tên gốc | hóa trị của gốc |
| \(HCl\) | axit clohidric | \(-Cl\) | clorua | 1 |
| \(HBr\) | axit bromhidric | \(-Br\) | bromua | 1 |
| \(H_2S\) | axit sùnuhidric | \(-HS\) \(=S\) | hidrosunfua sunfua | 1 2 |
| \(HNO_3\) | axit nitric | \(-NO_3\) | nitrat | 1 |

Ta có:\(\left(x-y\right)\left(x^2+xy+y^2\right)=x^3-y^3\)
với \(x=-10;y=2\) ,ta có:
\(\left(-10\right)^3-2^3=-1000-8=-1008\)
với \(x=-1;y=0\)
\(\left(-1\right)^3-0^3=-1-0=-1\)
với \(x=2;y=-1\) ,ta có:
\(2^3-\left(-1\right)^3=8-\left(-1\right)=8+1=9\)
với \(x=-0,5;y=1,25\), ta có:
\(\left(-0,5\right)^3-1,25^3=0-2=-2\)
Ta có bảng sau;
| Giá trị của x và y |
Giá trị của biểu thức \(\left(x-y\right)\left(x^2+xy+y^2\right)\) |
| \(x=-10;y=2\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=-1008\) |
| \(x=-1;y=0\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=-1\) |
| \(x=2;y=-1\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=9\) |
| \(x=-0,5;y=1,25\) | \(\left(x-y\right)\left(x^2+xy+y^2\right)=-2\) |
Trước hết, ta làm tính nhân để rút gọn biểu thức, ta được:
(x - y)(x2 + xy + y2) = x . x2 + x . xy + x . y2 + (-y) . x2 + (-y) . xy + (-y) . y2
= x3 + x2y + xy2 – yx2 – xy2 – y3 = x3 – y3
Sau đó tính giá trị của biểu thức x3 – y3
Ta có:
Khi x = -10; y = 2 thì A = (-10)3 – 23 = -1000 – 8 = 1008
Khi x = -1; y = 0 thì A = (-1)3 – 03 = -1
Khi x = 2; y = -1 thì A = 23 – (-1)3 = 8 + 1 = 9
Khi x = -0,5; y = 1,15 thì
A = (-0,5)3 – 1,253 = -0,125 – 1.953125 = -2,078125

\(\dfrac{x-1}{3}+\dfrac{5x-2}{2}=0\\ \Leftrightarrow2\left(x-1\right)+3\left(5x-2\right)=0\\ \Leftrightarrow2x-2+15x-6=0\\ \Leftrightarrow17x-8=0\\ \Leftrightarrow17x=8\\ \Leftrightarrow x=\dfrac{8}{17}\)
Vậy....................

1.
\(\dfrac{3}{5}=\dfrac{21}{35}\)
\(\dfrac{-7}{9}=\dfrac{-42}{54}\)
\(\dfrac{32}{48}=\dfrac{4}{6}\)
\(\dfrac{-36}{60}=\dfrac{-6}{10}\)
2.
\(\dfrac{26x}{13x^2}\) :NTC 13x
\(\dfrac{bc}{5b^2c^2}\) :NTC bc
\(\dfrac{ax^2}{2a^2x}\) :NTC ax
1
\(\dfrac{3}{5}=\dfrac{21}{35}\)
\(\dfrac{-7}{9}=\dfrac{-42}{54}\)
\(\dfrac{32}{48}=\dfrac{4}{6}\)
\(\dfrac{-36}{60}=\dfrac{-6}{10}\)
2

\(\frac{x+2}{x-3}-\frac{3}{x-3}=\frac{1}{x}\)
\(\Leftrightarrow\frac{x\left(x+2\right)-3x}{x\left(x-3\right)}=\frac{x-3}{x\cdot\left(x-3\right)}\)
\(\Leftrightarrow x^2+2x-3x-x+3=0\)
\(\Leftrightarrow x^2-2x+3=0\)
\(\Delta=\left(-2\right)^2-4.3=-8< 0\)
Vậy phương trình vô nghiệm.
\(\frac{x+2}{x-3}-\frac{3}{x-3}=\frac{1}{x}\)
\(\Leftrightarrow\frac{\left(x+2\right)x}{\left(x-3\right)x}-\frac{3x}{\left(x-3\right).x}=\frac{\left(x-3\right)}{\left(x-3\right).x}\)
\(\Rightarrow x^2+2x-3x=x-3\)
\(\Leftrightarrow x^2-x-x-3=0\)
\(\Leftrightarrow x^2-2x-3=0\)
\(\Leftrightarrow x^2+x-3x-3=0\)
\(\Leftrightarrow\left(x^2+x\right)-\left(3x+3\right)=0\)
\(\Leftrightarrow x\left(x+1\right)-3\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
Trong hình chữ nhật ABCD ta luôn có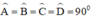
Do đó áp dụng định lý Py-ta-go ta có: d2 = a2 + b2.
Vậy :
- Cột thứ hai:
d2 = a2 + b2 = 52 + 122 = 25 + 144 = 169 nên d = 13
- Cột thứ ba:
a2 + b2 = d2 ⇒ a2 = d2 – b2 = (√10)2 – (√6)2 = 4 nên a = 2
- Cột thứ tư:
a2 + b2 = d2 ⇒ b2 = d2 – a2 = 72 – (√13)2 = 36 nên b = 6.
Vậy ta có bảng sau: