Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

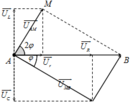
Biễu diễn vecto các điện áp. Mạch xảy ra cộng hưởng → U → cùng phương, chiều với vecto I → . Từ hình vẽ ta có:
U M B = U A M 2 + U 2 − 2 U A M U M B cos 2 φ
Mặc khác, áp dụng định lý sin trong tam giác AMB:
U sin 180 − 3 φ = U A M sin φ → sin 3 φ − 5 4 sin φ = 0
→ 4 sin 3 φ − 7 4 sin φ = 0
Phương trình cho ta nghiệm sin φ = 7 4 → φ ≈ 41 0 .
→ U M B = U A M 2 + U 2 − 2 U A M U M B cos 2 φ ≈ 240 V
Đáp án D

Khi L = L 1 thì dòng điện cùng pha với điện áp → hiện tượng cộng hưởng → Z C = Z L 1 = 2 π f L 1 .
Khi L = L 2 xảy ra cực đại điện áp hiệu dụng trên cuộn dây Z L 2 = R 2 + Z C 2 Z C ⇔ 2 π f L 2 = 50 2 + 2 π f L 1 2 2 π f L 1 → f = 25 Hz.
Đáp án A

Giải thích: Đáp án D
*Cường độ dòng điện tức thời trong mạch sớm pha so với điện áp tức thời hai đầu mạch nên mạch chứa đoạn RC mà không chứa RL.
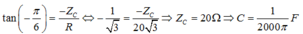

Chọn B
U RL = | · Z RL = U R 2 + Z L 2 R 2 + Z L - Z C 2 ∉ R ⇔ Z L 2 = Z L - Z C 2 ⇒ Z C = 2 Z L Z = R 2 + Z L 2 = U I = 100 Ω ⇒ Z L ≤ 100 Ω ⇒ Z C = 2 Z L ≤ 200 Ω ⇒ C ≥ 1 100 π 200 = 50 π 10 - 6 F

Chọn D
Ta có
R= U I R = 4U;
ZL = U I L = 2U;
ZC = U I C = 5U;
I = U Z = U U 4 2 + ( 2 - 5 ) 2
= 0,2A.

Đáp án A
L = L1, i cùng pha u => cộng hưởng ⇒ Z L 1 = Z C
L = L2, UL max ⇒ Z L 2 = R 2 + Z C 2 Z C
Để ý thấy L2 = 2L1. Thay R = 50 vào, ta có hệ: Z L 2 = 50 2 + Z C 2 Z C Z L 1 = Z C Z L 2 = 2 Z L 1 ⇔ Z L 1 = 50 Z L 2 = 100 Z C = 50 3
Từ đó dễ dàng tìm được f = 25(Hz).
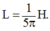
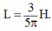
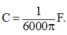

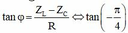
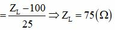

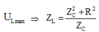
Từ điều kiện đề bài suy ra độ lệch pha của $i$ so với $u$ là
$\tan(\frac{\pi}{4})=\frac{Z_C-Z_L}{R}=1\Rightarrow C=\frac{1}{\omega(R+L\omega)}$
Mà $\omega=2\pi f$ nên $C=\frac{1}{2\pi f(R+2\pi Lf)}$
Từ điều kiện đề bài suy ra độ lệch pha của i so với u là
\(tan\left(\dfrac{\pi}{4}\right)=\dfrac{Z_C-Z_L}{R}=1\Rightarrow C=\dfrac{1}{w\left(R+Lw\right)}\)
Mà \(w=2\pi f\) nên \(C=\dfrac{1}{2\pi f\left(R+2\pi Lf\right)}\)