
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
* Với M là một điểm di động trên d 1 , N là một điểm di động trên d 2 thì MN ≤ d( d 1 ; d 2 )
Do đó, khoảng cách nhỏ nhất của MN chính là khoảng cách giữa hai đường thẳng d 1 và d 2 . Khi đó, MN là đoạn vuông góc chung của hai đường thẳng đã cho.
* Đường thẳng d 1 đi qua A(2; -2; 1), vecto chỉ phương u 1 → (3; 4; 1)
Đường thẳng d 2 đi qua B(7;3;9) vecto chỉ phương u 2 → (-2; -4; 2)
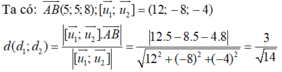
Chọn B.

Đáp án A
Khoảng cách nhỏ nhất giữa hai điểm A và B chính là khoảng cách giữa hai mặt phẳng (P) và (Q), dấu bằng xày ra khi và chỉ khi AB vuông góc với (P). Mặt khác vì O thuộc (P) nên ta có:
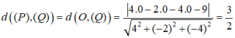
Vậy khoảng cách giữa hai điểm A và B nhỏ nhất bằng 3/2

Lời giải:
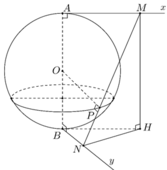
Gọi \(M\) là trung điểm của $AD$ . \(N\in AC\) sao cho \(AN=3a\).
Khi đó \(AB=AM=AN\). Do đó tứ xét tứ diện $ABNM$ thì chân đường cao hạ từ $A$ của tứ diện chính là tâm ngoại tiếp của \(\triangle BNM\)
Sử dụng định lý hàm cos suy ra \(BN=MN=BM=3a\)
Mặt khác dễ tính \(R=\sqrt{3}a\) ( $R$ là bán kính ngoại tiếp tam giác $BMN$ )
\(\Rightarrow h=\sqrt{AB^2-R^2}=\sqrt{6}a\)
\(\Rightarrow V_{ABNM}=\frac{1}{3}hS_{BNM}=\frac{9\sqrt{2}}{4}a^3\)
Theo công thức tỉ số thể tích:
\(\frac{V_{ABCD}}{V_{ABNM}}=\frac{AD.AB.AC}{AB.AM.AN}=6\Rightarrow V_{ABCD}=\frac{27\sqrt{2}}{2}a^3\)

Đáp án C
Ta có: II' = 6 = R + R'
Ta có: MN ≥ MI + II' + I'N = R + 6 + R' = 12
Dấu bằng xảy ra khi M, I, I', N theo thứ tự nằm trên một đường thẳng. Do đó M là giao điểm của tia đối của tia II' với mặt cầu (S), N là giao điểm của tia đối của tia I’I với mặt cầu (S’). Vậy đáp án đúng là C.
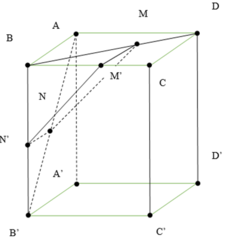
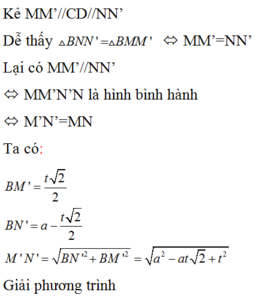
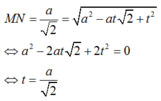
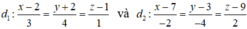

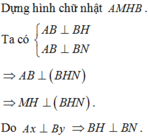
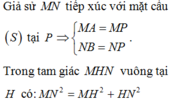
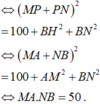
xxxxX==xx+x=X=