K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
7 tháng 7 2018
Phương pháp:
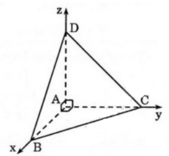
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc, khi đó ![]()
Cách giải:
![]()
Chọn: A

CM
2 tháng 1 2017
Phương pháp
Sử dụng công thức tính nhanh thể tích khối tứ diện biết ba cạnh và ba góc cùng xuất phát từ một đỉnh:
![]()
Cách giải:
Áp dụng công thức ![]()
ta được: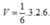
![]()
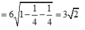
Chọn D.
PT
1

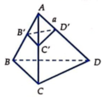
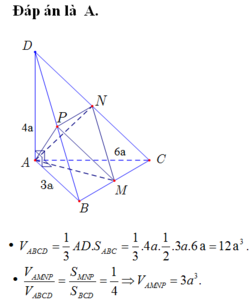
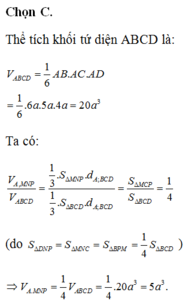

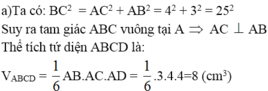
Lời giải:
Gọi \(M\) là trung điểm của $AD$ . \(N\in AC\) sao cho \(AN=3a\).
Khi đó \(AB=AM=AN\). Do đó tứ xét tứ diện $ABNM$ thì chân đường cao hạ từ $A$ của tứ diện chính là tâm ngoại tiếp của \(\triangle BNM\)
Sử dụng định lý hàm cos suy ra \(BN=MN=BM=3a\)
Mặt khác dễ tính \(R=\sqrt{3}a\) ( $R$ là bán kính ngoại tiếp tam giác $BMN$ )
\(\Rightarrow h=\sqrt{AB^2-R^2}=\sqrt{6}a\)
\(\Rightarrow V_{ABNM}=\frac{1}{3}hS_{BNM}=\frac{9\sqrt{2}}{4}a^3\)
Theo công thức tỉ số thể tích:
\(\frac{V_{ABCD}}{V_{ABNM}}=\frac{AD.AB.AC}{AB.AM.AN}=6\Rightarrow V_{ABCD}=\frac{27\sqrt{2}}{2}a^3\)