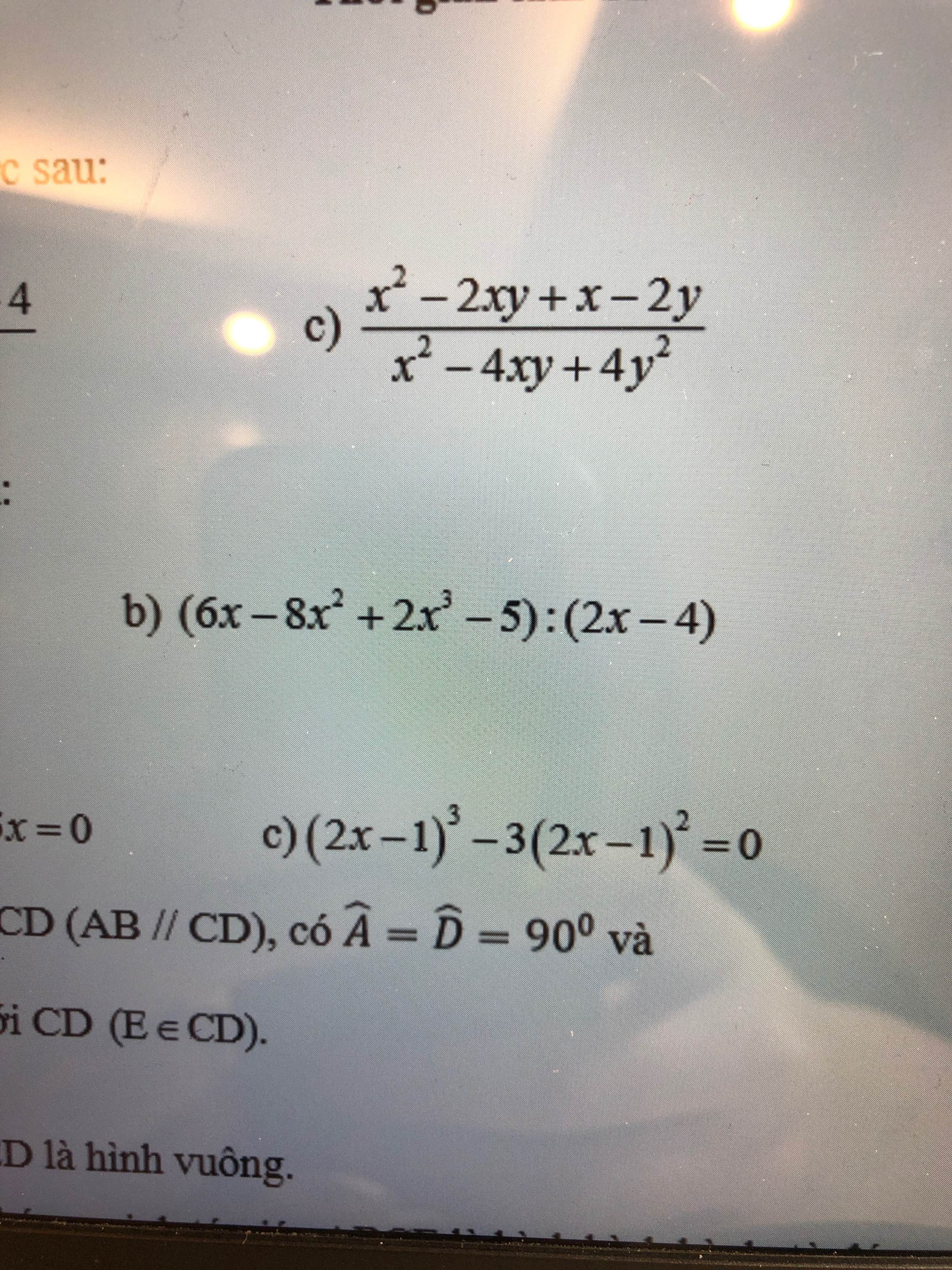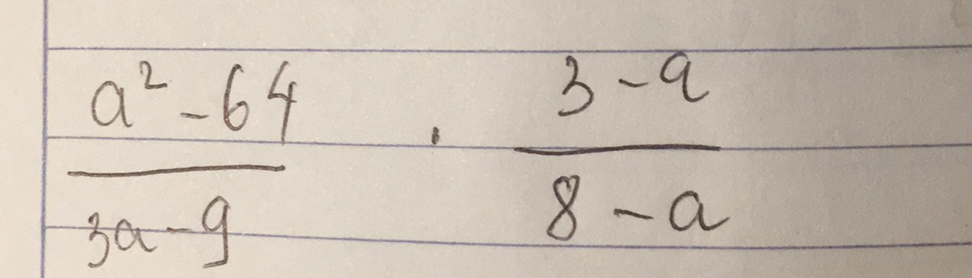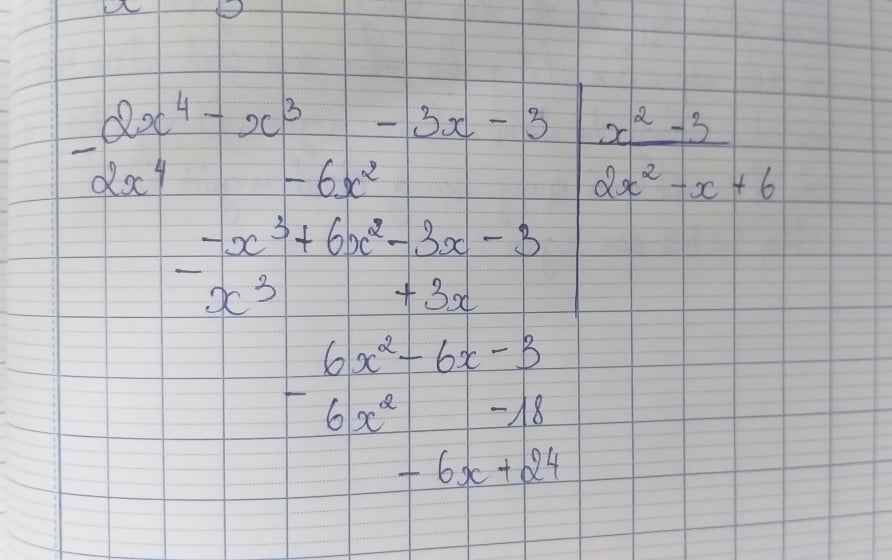K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
1
24 tháng 11 2021
\(2b,=\left(2x^3-4x^2-4x^2+8x-2x+4-9\right):\left(2x-4\right)\\ =\left[\left(2x-4\right)\left(x^2-2x-2\right)-9\right]:\left(2x-4\right)\\ =x^2-2x-2\left(\text{ dư -9}\right)\)
TS
1
29 tháng 6 2023
\(\text{∘}\) \(\text{Ans}\)
\(\downarrow\)
\(14x^2y^3-7xy^2\cdot\left(2x-3y\right)\)
`=`\(14x^2y^3-\left[7xy^2\cdot2x+7xy^2\cdot\left(-3y\right)\right]\)
`=`\(14x^2y^3-\left(14x^2y^2-21xy^3\right)\)
`=`\(14x^2y^3-14x^2y^2+21xy^3\)
\(\text{∘}\) \(\text{Kaizuu lv uuu.}\)
Q0
2
4 tháng 7 2021
(x - 3)3 - (x + 1)3 + 12x (x - 1)
= x3 - 3x2 . 3 + 3x . 32 - 27 - (x3 + 3x2 . 1 + 3x . 12 + 13) + 12x . x + 12x . (-1)
= x3 - 9x2 + 27x - 27 - x3 - 3x2 - 3x - 1 + 12x2 - 12x
= (x3 - x3) + (12x2 - 9x2 - 3x2) + (27x - 3x - 12x) - (27 + 1)
= 12x - 28
4 tháng 7 2021
\(\left(x-3\right)^3-\left(x+1\right)^3+12x\left(x-1\right)\)
\(\Leftrightarrow\left(x^3-3x^23+3x3^2-3^3\right)-\left(x^3+3x^21+3x1^2+1^3\right)+12x^2-12x\)
\(\Leftrightarrow x^3-9x^2+27x-27-x^3-3x^2-3x-1+12x^2-12x\)
\(\Leftrightarrow12x-28=0\)
\(\Leftrightarrow12x=28\)
\(\Leftrightarrow x=\frac{7}{3}\)
Vậy S={\(\frac{7}{3}\)} là nghiệm pt
Q0
1
MH
25 tháng 11 2021
\(\dfrac{a^2-64}{3a-9}.\dfrac{3-a}{8-a}\)
\(=\dfrac{a^2-8^2}{3\left(a-3\right)}.\dfrac{a-3}{a-8}\)
\(=\dfrac{\left(a+8\right)\left(a-8\right)}{3\left(a-3\right)}.\dfrac{a-3}{a-8}\)
\(=\dfrac{\left(a+8\right)\left(a-8\right)\left(a-3\right)}{3\left(a-3\right)\left(a-8\right)}\)
\(=\dfrac{a+8}{3}\)
NN
2
NN
1
NN
0
NN
15 tháng 8 2018
Trong hình thang ABCD có: AE=ED(...)
BF=FC(...)
suy ra EF là đường trung bình của hình thang ABCD
suy ra EF//AB//DC suy ra EF//CD (1)
Trong tam giác ADC có: AE=ED(..)
AM=MC(...)
suy ra EM là đường trung bình của tam giác ADC
suy ra EM//CD (2)
Trong tam giác BDC co BN=ND(...)
BF=FC(...)
suy ra FN là đường trung bình của tam giác BDC
suy ra NF//CD(3)
Từ (1);(2) và (3) suy ra
E;N;M;E thẳng hàng
Vì EM là đường trung bình của tam giác ADC (cmt) nên \(EM=\frac{1}{2}CD\)
Trong tam giác ABD có: AE=DE(...)
DN=BN(....)
do đó EN là đường trung bình của tam giác ABD
\(\Rightarrow EN=\frac{1}{2}AB\)
Ta có NE+MN=EM
\(\Rightarrow MN=EM-NE=\frac{1}{2}CD-\frac{1}{2}AB=\frac{1}{2}\left(CD-AB\right)\)