
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()
![]()
![]()

\(g\left(x\right)=f\left(1-2018x\right)\Rightarrow g'\left(x\right)=-2018f'\left(1-2018x\right)\)
\(\Rightarrow\) Số nghiệm của \(g'\left(x\right)\) bằng số nghiệm \(f'\left(x\right)\Rightarrow g'\left(x\right)\) có 4 nghiệm
\(g\left(x\right)=0\Leftrightarrow f\left(1-2018x\right)=0\) có số nghiệm bằng số nghiệm f(x)
Do \(f'\left(x\right)\) có 4 nghiệm nên f(x) có tối đa 5 nghiệm
Vậy hàm có tối đa 9 cực trị

Đáp án D.
Tập xác định D = R.
Ta có y’ = x2 – 4x + 3, y’ = 0
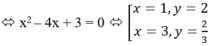
Bảng biến thiên
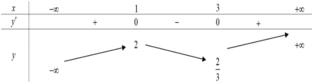
Tọa độ điểm cực đại của hàm số là (1;2).

a)Cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm:
Quy tắc 1:
1. Tìm tập xác định.
2. Tính f'(x). Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.
3. Lập bảng biến thiên.
4. Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2:
1. Tìm tập xác định.
2. Tính f'(x). Giải phương trình f'(x) = 0 và kí hiệu xi (i = 1, 2, 3, ...) là các nghiệm của nó.
3. Tính f"(x) và f"(xi)
4. Nếu f"(xi) > 0 thì xi là điểm cực tiểu.
Nếu f"(xi) < 0 thì xi là điểm cực đại.
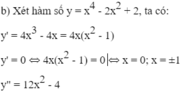
Dựa vào Quy tắc 2, ta có:
y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại.
y"(-1) = y"(1) = 8 > 0 ⇒ x = ±1 là hai điểm cực tiểu.