Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)

1. \(y'=3x^2\sqrt{x}+\dfrac{x^3-5}{2\sqrt{x}}=\dfrac{7x^3-5}{2\sqrt{x}}\)
2. \(y'=3x^5+\dfrac{3}{x^2}+\dfrac{1}{\sqrt{x}}\)
3. \(y'=2-\dfrac{2}{\left(x-2\right)^2}\)

Ta có
f ( x ) = ( x + 2 ) ( x − 3 ) = x 2 − x − 6 ⇒ f ' x = 2 x − 1
Chọn đáp án C

a: \(y'=4\cdot3x^2-3\cdot2x+2=12x^2-6x+2\)
b: \(y'=\dfrac{\left(x+1\right)'\left(x-1\right)-\left(x+1\right)\left(x-1\right)'}{\left(x-1\right)^2}=\dfrac{x-1-x-1}{\left(x-1\right)^2}=\dfrac{-2}{\left(x-1\right)^2}\)
c: \(y'=-2\cdot\left(\sqrt{x}\cdot x\right)'\)
\(=-2\cdot\left(\dfrac{x+x}{2\sqrt{x}}\right)=-2\cdot\dfrac{2x}{2\sqrt{x}}=-2\sqrt{x}\)
d: \(y'=\left(3sinx+4cosx-tanx\right)\)'
\(=3cosx-4sinx+\dfrac{1}{cos^2x}\)
e: \(y'=\left(4^x+2e^x\right)'\)
\(=4^x\cdot ln4+2\cdot e^x\)
f: \(y'=\left(x\cdot lnx\right)'=lnx+1\)

1) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
2) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1\left(x+9\right)}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{-6}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(1\right)=\dfrac{-6}{\left(1+3\right)^2}+\dfrac{2}{\sqrt[]{1}}=-\dfrac{3}{8}+2=\dfrac{13}{8}\)

a) Cách 1: y' = (9 -2x)'(2x3- 9x2 +1) +(9 -2x)(2x3- 9x2 +1)' = -2(2x3- 9x2 +1) +(9 -2x)(6x2 -18x) = -16x3 +108x2 -162x -2.
Cách 2: y = -4x4 +36x3 -81x2 -2x +9, do đó
y' = -16x3 +108x2 -162x -2.
b) y' = .(7x -3) +
(7x -3)'=
(7x -3) +7
.
c) y' = (x -2)'√(x2 +1) + (x -2)(√x2 +1)' = √(x2 +1) + (x -2) = √(x2 +1) + (x -2)
= √(x2 +1) +
=
.
d) y' = 2tanx.(tanx)' - (x2)' =
.
e) y' = sin
=
sin
.

a/ \(y=\left(x^3-3x\right)^{\dfrac{3}{2}}\Rightarrow y'=\dfrac{3}{2}\left(x^3-3x\right)^{\dfrac{1}{2}}\left(x^3-3x\right)'=\dfrac{3}{2}\left(3x^2-3\right)\sqrt{x^3-3x}\)
b/ \(y'=5\left(\sqrt{x^3+1}-x^2+2\right)^4\left(\sqrt{x^3+1}-x^2+2\right)'=5\left(\sqrt{x^3+1}-x^2+2\right)^4\left(\dfrac{3x^2}{\sqrt{x^3+1}}-2x\right)\)c/
\(y'=14\left(x^6+2x-3\right)^6\left(x^6+2x-3\right)'=14\left(x^6+2x-3\right)^6\left(6x^5+2\right)\)
d/ \(y=\left(x^3-1\right)^{-\dfrac{5}{2}}\Rightarrow y'=-\dfrac{5}{2}\left(x^3-1\right)^{-\dfrac{7}{2}}\left(x^3-1\right)'=-\dfrac{15x^2}{2\sqrt{\left(x^3-1\right)^7}}\)
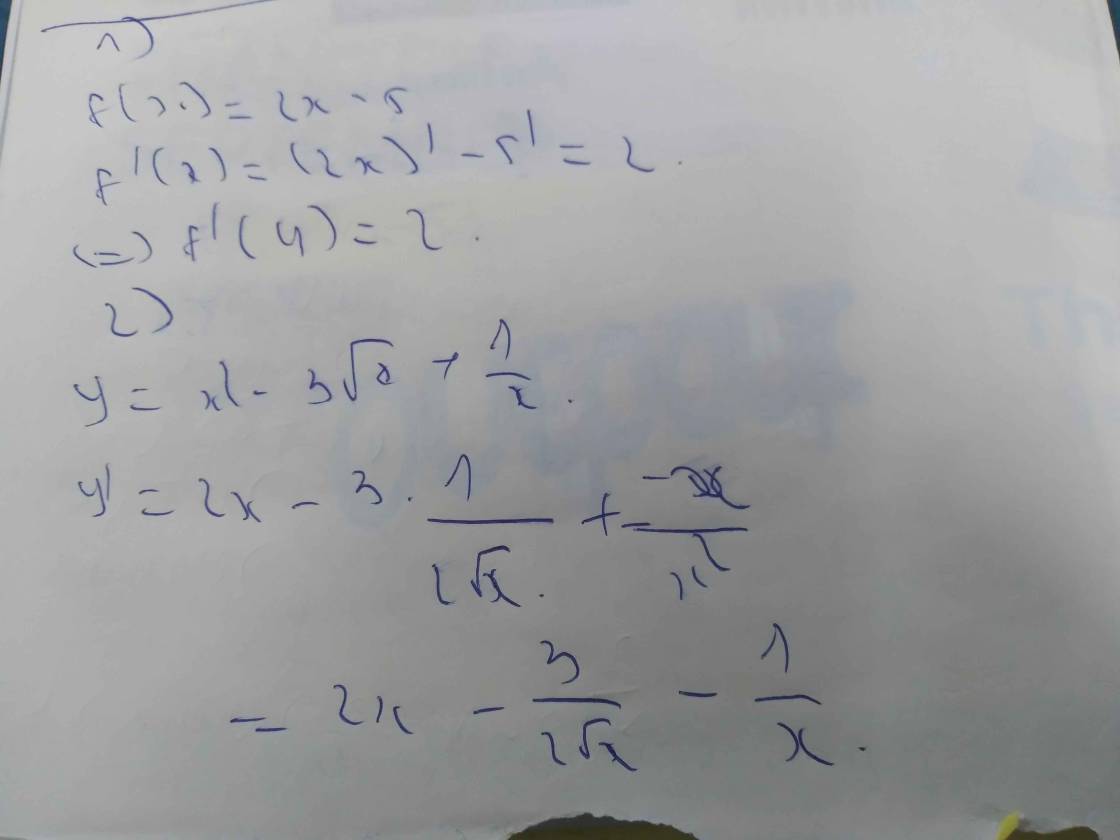

Áp dụng công thức u n ' = n u n − 1 . u ' .
Ta có
y ' = 2 x 5 − 2 x 2 x 5 − 2 x 2 ' = 2 x 5 − 2 x 2 5 x 4 − 4 x
= 2 ( 5 x 9 − 4 x 6 − 10 x 6 + 8 x 3 ) = 2 ( 5 x 9 − 14 x 6 + 8 x 3 ) = 10 x 9 − 28 x 6 + 16 x 3
Chọn đáp án C