
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
a; \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) = \(\dfrac{5}{20}\) - \(\dfrac{4}{20}\) = \(\dfrac{1}{20}\)
b; \(\dfrac{3}{5}\) - \(\dfrac{-1}{2}\) = \(\dfrac{6}{10}\) + \(\dfrac{5}{10}\) = \(\dfrac{11}{10}\)
c; \(\dfrac{3}{5}\) - \(\dfrac{-1}{3}\) = \(\dfrac{9}{15}\) + \(\dfrac{5}{15}\) = \(\dfrac{14}{15}\)
d; \(\dfrac{-5}{7}\) - \(\dfrac{1}{3}\)= \(\dfrac{-15}{21}\) - \(\dfrac{7}{21}\)= \(\dfrac{-22}{21}\)
Bài 5
a; 1 + \(\dfrac{3}{4}\) = \(\dfrac{4}{4}\) + \(\dfrac{3}{4}\) = \(\dfrac{7}{4}\) b; 1 - \(\dfrac{1}{2}\) = \(\dfrac{2}{2}\) - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\)
c; \(\dfrac{1}{5}\) - 2 = \(\dfrac{1}{5}\) - \(\dfrac{10}{5}\) = \(\dfrac{-9}{5}\) d; -5 - \(\dfrac{1}{6}\) = \(\dfrac{-30}{6}\) - \(\dfrac{1}{6}\) = \(\dfrac{-31}{6}\)
e; - 3 - \(\dfrac{2}{7}\)= \(\dfrac{-21}{7}\) - \(\dfrac{2}{7}\)= \(\dfrac{-23}{7}\) f; - 3 + \(\dfrac{2}{5}\) = \(\dfrac{-15}{5}\) + \(\dfrac{2}{5}\)= - \(\dfrac{13}{5}\)
g; - 3 - \(\dfrac{2}{3}\) = \(\dfrac{-9}{3}\) - \(\dfrac{2}{3}\) = \(\dfrac{-11}{3}\) h; - 4 - \(\dfrac{-5}{7}\) = \(\dfrac{-28}{7}\)+ \(\dfrac{5}{7}\) = - \(\dfrac{23}{7}\)

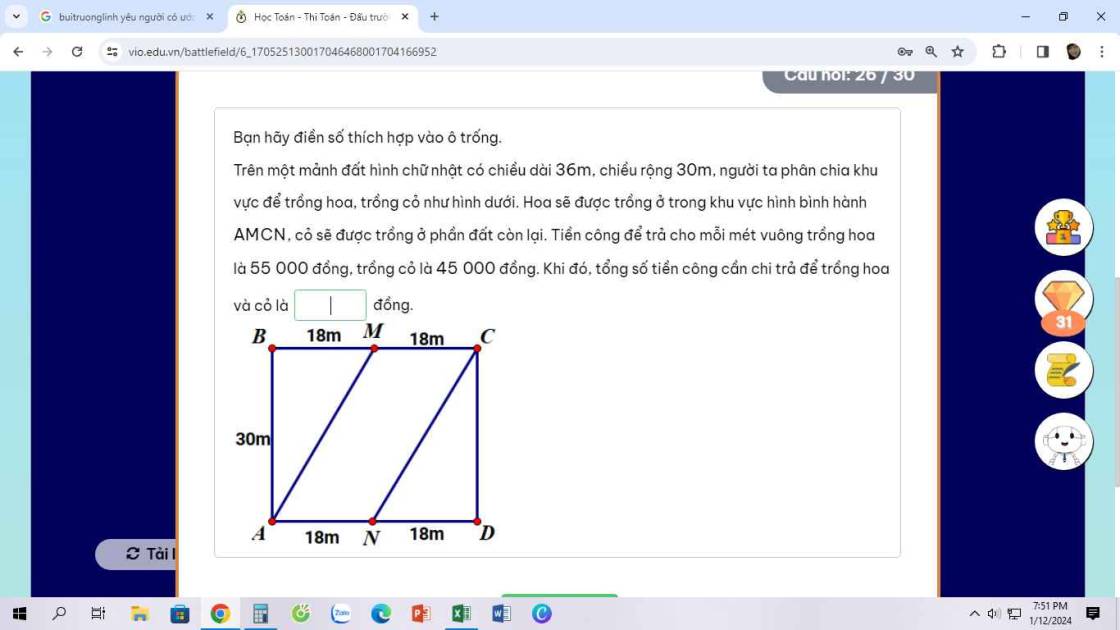
Diện tích mảnh đất là:
\(30\times\left(18+18\right)=1080\left(m^2\right)\)
Diện tích trồng hoa là:
\(30\times18=540\left(m^2\right)\)
Diện tích trồng cỏ là:
\(1080-540=540\left(m^2\right)\)
Tổng tiền cần chi trả là:
\(55000\times540+45000\times540=54000000\) (đồng)
Giải
Diện tích mảnh đất là:
30x(18+18)=1080(m vuông)
Diện tích trồng hoa là:
30x18=540(m vuông)
Diện tích trồng cỏ là:1080-540=540(m vuông)
Tổng số tiền cần chị trả là:
55000x540+45000x540=54000000(đồng)
Chúc bạn học tốt!

BÀi 1:
\(\dfrac{\overline{abab}}{\overline{cdcd}}\) = \(\dfrac{\overline{abab:}101}{\overline{cdcd}:101}\) = \(\dfrac{\overline{ab}}{cd}\)
\(\dfrac{\overline{abcabc}}{\overline{abc}}\) = \(\dfrac{\overline{abc}\times1001}{\overline{abc}}\) = 1001


Bài 5:
a. Gọi $d=ƯCLN(n-2, n+1)$
$\Rightarrow n-2\vdots d; n+1\vdots d$
$\Rightarrow (n+1)-(n-2)\vdots d$
$\Rightarrow 3\vdots d\Rightarrow d\in \left\{1; 3\right\}$
Để ps tối giản thì $n-2\not\vdots 3$
$\Leftrightarrow n\neq 3k+2$ với $k$ là số tự nhiên bất kỳ.
b.
Gọi $d=ƯCLN(n+5, n-2)$
$\Rightarrow n+5\vdots d; n-2\vdots d$
$\Rightarrow (n+5)-(n-2)\vdots d$
$\Rightarrow 7\vdots d$
$\Rightarrow d\in \left\{1; 7\right\}$
Để ps tối giản thì $n-2\not\vdots 7$
$\Rightarrow n\neq 7k+2$ với $k$ là số tự nhiên bất kỳ.

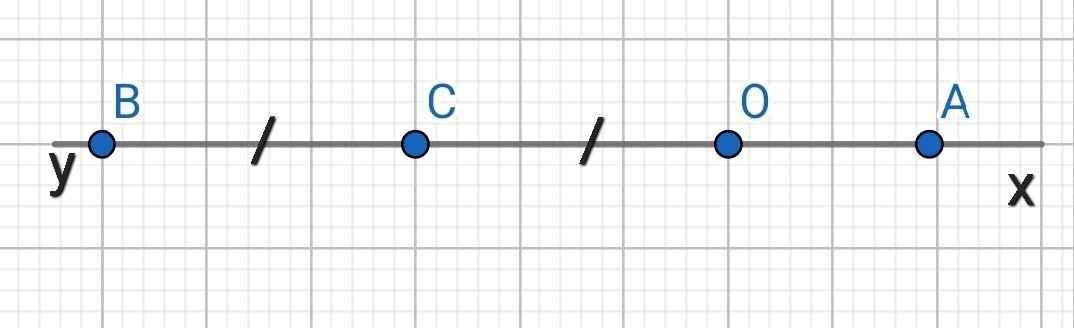 Do C là trung điểm của OB
Do C là trung điểm của OB
⇒ OC = OB : 2 = 6 : 2 = 3 (cm)
⇒ OC > OA
⇒ O không là trung điểm của AC

Có quá nhiều bài, thứ nhất em đăng tách ra, thứ hai chụp gần cận cho rõ, thứ ba em chỉ đăng bài cần giúp


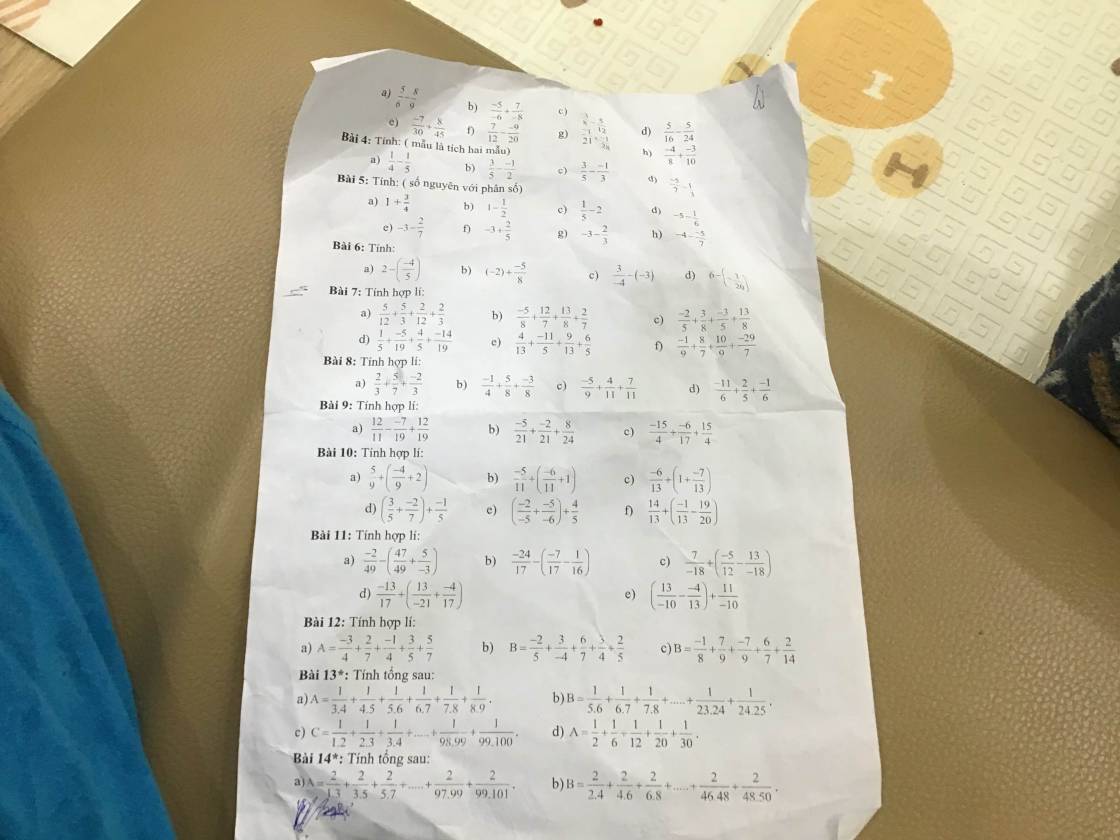
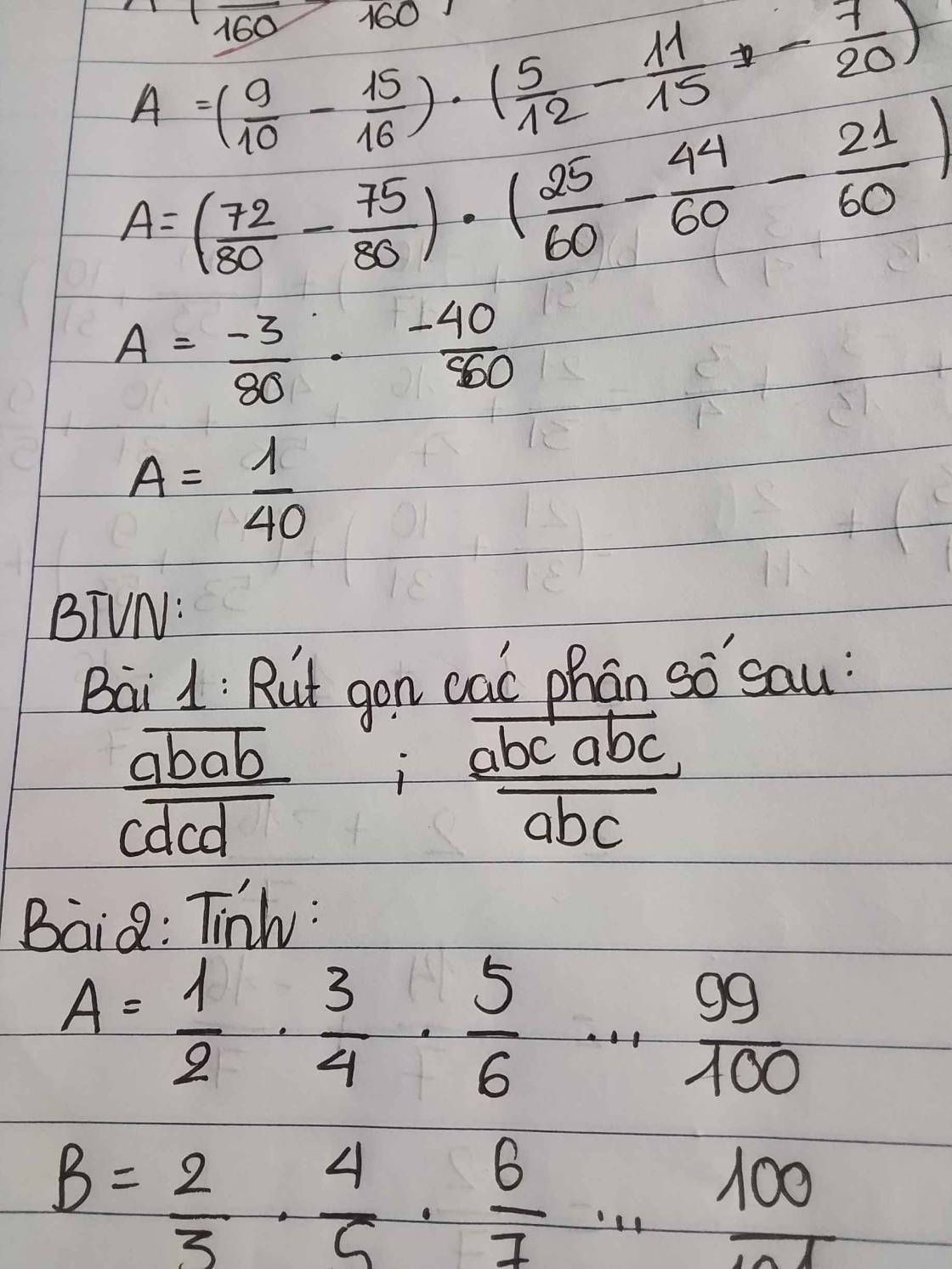 giải giúp mình bài 1 vs ạ
giải giúp mình bài 1 vs ạ


Bài 1:
a) \(4x+y+xy=5\)
\(\Leftrightarrow4x+4+\left(y+xy\right)=9\)
\(\Leftrightarrow4\left(x+1\right)+y\left(x+1\right)=9\)
\(\Leftrightarrow\left(x+1\right)\left(y+4\right)=9\)
mà \(x,y\) là các số tự nhiên nên \(x+1,y+4\) là các ước dương của \(9\), mà \(y+4\ge4\) nên
\(\left\{{}\begin{matrix}x+1=1\\y+4=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=5\end{matrix}\right.\) (thỏa mãn).
b) \(2x+xy+y=7\)
\(\Leftrightarrow2x+2+\left(xy+y\right)=9\)
\(\Leftrightarrow2\left(x+1\right)+y\left(x+1\right)=9\)
\(\Leftrightarrow\left(x+1\right)\left(y+2\right)=9\)
mà \(x,y\) là các số tự nhiên nên \(x+1,y+2\) là các ước dương của \(9\).
Ta có bảng giá trị:
Vậy có các cặp \(\left(x;y\right)\) thỏa mãn là \(\left(0;7\right),\left(2,1\right)\).
c) \(4x+xy+2y=5\)
\(\Leftrightarrow4x+8+\left(xy+2y\right)=13\)
\(\Leftrightarrow4\left(x+2\right)+y\left(x+2\right)=13\)
\(\Leftrightarrow\left(x+2\right)\left(y+4\right)=13\)
mà \(x,y\) là các số tự nhiên nên \(x+2,y+4\) là các ước dương của \(13\).
Ta có bảng giá trị:
Vậy không có giá trị nào của \(\left(x;y\right)\) thỏa mãn ycbt.
Bài 2:
Gọi ba số tự nhiên chẵn liên tiếp là \(2a,2a+2,2a+4\) (\(a\inℕ\))
Vì tổng của hai số bé lớn hơn số lớn là \(22\) nên ta có:
\(\left[2a+\left(2a+2\right)\right]-\left(2a+4\right)=22\)
\(\Leftrightarrow2a=24\)
\(\Leftrightarrow a=12\) .
Vậy ba số cần tìm là \(24,26,28\).