Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

rối quá :)
B = (-5)0 + 51 + (-5)2 + 53 + ... + (-5)2016 + 52017
B = 1 + 51 + 52 + 53 + ... + 52016 + 52017
5B = 5 + 52 + 53 + ... + 52016 + 52017
5B - B = (5 + 52 + 53 + ... + 52016 + 52017) - (1 + 51 + 52 + 53 + ... + 52016 + 52017)
4B = 52017 - 1
B = \(\dfrac{5^{2017}-1}{4}\)
a) Tìm GTNN :A=|3x -2017|+6
B=1/2(3x-1/8)mũ 4 -1/6
b)Tìm GTLN :C=3-(x+1)mũ 2 -2|y-7|
D=16-(4x-3)mũ 2

a) Ý 1: Ta có:
/3x - 2017/ \(\ge\) 0 \(\forall\)x \(\in\) Z
=> /3x - 2017/ + 6 \(\ge\) 0 \(\forall\)x \(\in\) Z
=> A \(\ge\) 0 \(\forall\)x \(\in\) Z
Dấu "=" xảy ra khi /3x - 2017/ = 0
=> 3x - 2017 = 0
=> 3x = 2017
=> x = \(\frac{2017}{3}\)
Vậy GTNN của A = 6 khi x = \(\frac{2017}{3}\)
b) Lại có: -(4x - 3)2 \(\ge\) 0
=> 16 - (4x - 3)2 \(\ge\) 16 \(\forall\)x \(\in\) Z
=> D \(\ge\) 16 \(\forall\)x \(\in\) Z
Dấu "=" xảy ra khi (4x - 3)2 = 0
=> 4x - 3 = 0
=> 4x = 3 => x = \(\frac{3}{4}\)
Vậy GTLN của D = 16 khi x = \(\frac{3}{4}\).

\(A=1+2+2^2+...+2^{2017}\)
\(\Rightarrow A=\dfrac{2^{2017+1}-1}{2-1}\)
\(\Rightarrow A=2^{2018}-1\)
mà \(B=2^{2018}\)
\(\Rightarrow A-B=2^{2018}-1-2^{2018}\)
\(\Rightarrow A-B=-1\)
\(2A=2+2^2+2^3+...+2^{2018}\)
\(\Rightarrow A=2A-A=2^{2018}-1\)
\(\Rightarrow A-B=2^{2018}-1-2^{2018}=-1\)

a) Lập bảng
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
| 7n | 7 | 9 | 3 | 1 | 7 | 9 | 3 | 1 | ... |
| 9n | 9 | 1 | 9 | 1 | 9 | 1 | 9 | 1 | ... |
Ta có: 2018 : 4 = 504 (dư 2)
Suy ra \(2017^{2018}+2019^{2018}= \overline{...9}+\overline{...1}=\overline{...0}\)
Vậy 20172018 + 20192018 chia hết cho 10
b) Làm tương tự như câu a)

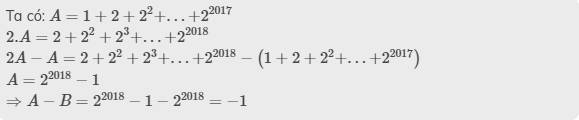
Từ \(\frac{a}{b}=\frac{c}{d}\)\(\Rightarrow\frac{a}{c}=\frac{b}{d}\)\(\Rightarrow\left(\frac{a}{c}\right)^{2017}=\left(\frac{b}{d}\right)^{2017}=\frac{a^{2017}}{c^{2017}}=\frac{b^{2017}}{d^{2017}}=\frac{a^{2017}+b^{2017}}{c^{2017}+d^{2017}}=\frac{a^{2017}-b^{2017}}{c^{2017}-d^{2017}}\left(đpcm\right)\)
Cảm ơn bạn nhiều !