
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(VT=\left(\frac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\frac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(-\sqrt{7}-\sqrt{5}\right).\left(\sqrt{7}-\sqrt{5}\right)=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
\(=-\left(7-5\right)=-2=VP\left(đpcm\right)\)
Lời nói chẳng mất tiền mua. Lựa lời mà chửi cho vừa lòng nhau. Đã chửi, phải chửi thật đau. Chửi mà hiền quá còn lâu nó chừa. Chửi đúng , không được chửi bừa . Chửi cha mẹ nó , không thừa một ai . Khi chửi , chửi lớn mới oai. Chửi hay là phải chửi dài , chửi lâu . Chửi đi chửi lại mới ngầu. Chửi nhiều cho nó nhức đầu , đau tai. Chửi xong nhớ nói bái bai . Phóng nhanh kẻo bị ăn chai vào mồm.

C = 1
H = 2
A = 3
O = 4
M = 5
U = 6
N = 7
G = 8
20 - 11 = 9
=> Chào mừng 20/11

Cách 3 :
\(a+b+c\ge2+abc\Leftrightarrow\left(a+b+c\right)\left(ab+bc+ca\right)\ge6+3abc\)
Từ điều kiện ta có thể suy ra : \(a+b+c\ge3\)
Từ đó ta có : \(6\le\frac{2}{3}\left(a+b+c\right)\left(ab+bc+ca\right)\)
Đến đây ta cần chứng minh : \(\left(a+b+c\right)\left(ab+bc+ca\right)\ge\frac{2}{3}\left(a+b+c\right)\left(ab+bc+ca\right)+3abc\)
\(\Leftrightarrow\left(a+b+c\right)\left(ab+bc+ca\right)\ge9abc\)(Đây là hệ quả của Cô-si)
Ta có: \(a^2+b^2+c^2\ge ab+bc+ac\ge3\sqrt[3]{a^2b^2+b^2c^2+c^2a^2}\)
=> \(\hept{\begin{cases}a^2+b^2+c^2\ge3\\1\ge abc\end{cases}}\)
Có: \(\left(a+b+c\right)^2=a^2+b^2+c^2+2\left(ab+bc+ac\right)\ge3+6=9\)
=> \(a+b+c\ge3=2+1\ge2+abc\)


thì chứng minh 4 điểm ý cùng thuộc đường thẳng đường kính nào đó!
hay pạn ra bài cụ thể đi!

E mới hk lớp 8 nên chỉ thử có j thông cảm!!
Giả sử tồn tại số tự nhiên n thỏa mãn \(n^2+3n+5⋮121\)
=> \(4\left(n^2+3n+5\right)⋮121\)
=> \(\left(4n^2+12n+9\right)+11⋮121\)
=> \(\left(2n+3\right)^2+11⋮121\)
Vì \(4\left(n^2+3n+5\right)⋮11\) ( vì \(121⋮11\)) và \(11⋮11\)
=> \(\left(2n+3\right)^2⋮11\)
=> \(\left(2n+3\right)^2⋮121\) ( vì 11 là số nguyên tố)
=> \(\left(2n+3\right)^2+11\) không chia hết cho 121 ( vì 11 không chia hết cho 121)
hay \(4\left(n^2+3n+5\right)\) không chia hết cho 121
=> \(n^2+3n+5\) ko chia hết cho 121 ( vì 4 và 121 nguyên tố cùng nhau) ( đpcm)

Huhu mình mới thi về mà sock quá😭 thấy nhiều người vẽ sai lắm ạ! Chắc tầm 1/3 khối!
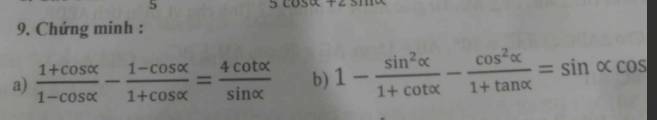 chứng minh theo kiểu vt=... = vp(dpcm) giúp mình với
chứng minh theo kiểu vt=... = vp(dpcm) giúp mình với

\(a,VT=\dfrac{1+cos\alpha}{1-cos\alpha}-\dfrac{1-cos\alpha}{1+cos\alpha}=\dfrac{\left(1+cos\alpha\right)^2-\left(1-cos\alpha\right)^2}{1^2-cos\alpha^2}\\ =\dfrac{1+2cos\alpha+cos^2\alpha-1+2cos\alpha-cos^2\alpha}{sin^2\alpha}\\ =\dfrac{4cos\alpha}{sin^2\alpha}\\ =4\left(\dfrac{cos\alpha}{sin\alpha}:\dfrac{sin^2\alpha}{sin\alpha}\right)\\ =\dfrac{4cot\alpha}{sin\alpha}=VP\left(dpcm\right)\)
cảm ơn b nha <3