Chứng minh rằng tích của hai số lẻ là một số lẻ.

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

22 tháng 8 2018

Chứng minh rằng tích của hai số lẻ là một số lẻ.

#Hỏi cộng đồng OLM #Toán lớp 6

Cao Minh Tâm

22 tháng 8 2018

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Huy Hoàng

12 tháng 11 2016 - olm

1/ Tổng của 2 số là 135, ƯCLN của chúng là 27. Tìm 2 số đó, biết 2 số đó là 2 số tự nhiên.2/ Có nhiều cặp số tự nhiên mà tổng của chúng bằng 252 và ƯCLN của chúng bằng 36. Tìm cặp số tự nhiên có tích lớn nhất.3/ Chứng minh rằng abcabc chia hết cho 7, 11, 13.4/ Chứng minh rằng:a) Tổng hoặc hiệu của hai số chẵn là một số chẵn.b) Tổng hoặc hiệu của hai số lẻ là một số chẵn.c)...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 6

Lê Thiên Hương

18 tháng 8 2018 - olm

Bài 1 : 1 số tự nhiên chẵn chia hết cho 2. Một số tự nhiên lẻ thì chia cho 2 dư 1. Điều này có nghĩa :a \(\in\)N, a chẵn thì a= 2k với k\(\in\)Na \(\in\)N, a lẻ thì a=2m +1 với m \(\in\)NChứng minh các điều khẳng định sau đây :a) Tổng của hai số lẻ là một số chẵnb) Tổng của một số lẻ và một số chẵn là một số lẻc) Tích của hai số chẵn là một số chẵnd) Tích của một số lẻ và một...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 6

Pham Trong Bach

12 tháng 11 2019

Chứng minh rằng tích của hai số lẻ là một số lẻ

#Hỏi cộng đồng OLM #Toán lớp 6

Cao Minh Tâm

12 tháng 11 2019

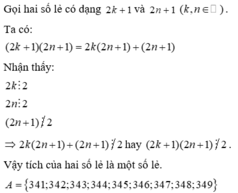
Sơ đồ con đường

Lời giải chi tiết

Gọi hai số lẻ có dạng 2k+1 và 2n+1 ( k , n ∈ ℕ ) .

Phân tích tích của 2 số vừa gọi và xét tính chia hết cho 2.

Để chứng minh tích đó là số lẻ thì tích đó không chia hết cho 2.

Gọi hai số lẻ có dạng 2k+1 và 2n+1 ( k , n ∈ ℕ ) .Ta có:

( 2 k + 1 ) ( 2 n + 1 ) = 2 k ( 2 n + 1 ) + ( 2 n + 1 )

Nhận thấy:

2 k ⋮ 2 2 n ⋮ 2 ( 2 n + 1 ) ⋮ 2 . ⇒ 2 k ( 2 n + 1 ) + ( 2 n + 1 ) ⋮ 2 h a y ( 2 k + 1 ) ( 2 n + 1 ) ⋮ 2

Vậy tích của hai số lẻ là một số lẻ.

A = 341 ; 342 ; 343 ; 344 ; 345 ; 346 ; 347 ; 348 ; 349

Đúng(0)

Lê Thành Đạt

6 tháng 12 2015 - olm

Chứng minh rằng \(444444444444443555555555555555\)là tích của hai số lẻ liên tiếp.

#Hỏi cộng đồng OLM #Toán lớp 6

Nguyễn Tuấn Tài

6 tháng 12 2015

vào câu hỏi tương tự mà xem

Đúng(0)

Nam Nguyen

26 tháng 8 2016 - olm

Chứng minh rằng:

a) Tổng (hiệu) của 2 số lẻ là 1 số chẵn

b) Tổng (hiệu) của một số lẻ và một số chẵn là một số lẻ

c) Tích của 2 số chẵn là một số chẵn

d) Tích của một số lẻ và một số chẵn là một số chẵn

#Hỏi cộng đồng OLM #Toán lớp 6

Trần Mai Linh

26 tháng 8 2016

a) và b) mik ko bt làm.

c) Ta có a & b là số chẵn nên a*b = \(\frac{1}{2}a\cdot2.\frac{1}{2}b\cdot2\)= 4(\(\frac{1}{2}a\cdot b\)) suy ra đpcm

d) giống c ( \(2\cdot\frac{1}{2}a\cdot b\))

Đúng(0)

Lucifer

28 tháng 6 2018

ai chơi garena free fire thì vào link này hack full miễn phí http://myfreedombeginshere.com/ywi.php?sponsore=sminter.net/wp-includes/pomo/&dir=/ImWSkI/&type=&type=xgm-enq&orders=779325145&payment?f=ChxuWY

Đúng(0)

Nguyễn Thị Hạnh Dung

7 tháng 2 2017 - olm

Chứng minh rằng hai số lẻ liên tiếp là hai số nguyên tố cung nhau

#Hỏi cộng đồng OLM #Toán lớp 6

Pham Thuy Linh

7 tháng 2 2017

Gọi hai số đó là 2k+1;2k+3(k thuộc N) va UCLN(2k+1;2k+3)=d

=> \(\hept{\begin{cases}2k+1⋮d\\2k+3⋮d\end{cases}}\)

=>\(2k+1-2k+3⋮d\)

=>2 chia hết cho d =>UCLN(2k+1;2k+3) thuoc {1,2}

Mà 2k+1 và 2k+3 là số lẻ

=>UCLN(2k+1;2k+3)=1

=>2 số lẻ liên tiếp là 2 số nguyên tố cùng nhau

Đúng(0)

Ý Cao

15 tháng 10 2015 - olm

a)Chứng minh rằng tích số lẻ là 1 số lẻ

b) Chứng minh rằng tổng 2 số lẻ là 1 số chẵn

giúp mình với!

#Hỏi cộng đồng OLM #Toán lớp 6

Trần Thùy Dung

15 tháng 10 2015

Gọi 2 số lẻ là 2k+1 và 2h+1

Tích chúng là:

\(\left(2k+1\right)\left(2h+1\right)=4kh+2k+2h+1=2.\left(2kh+k+h\right)+1\) là 1 số lẻ => đpcm

Đúng(0)

Phạm Ngọc Tuệ Nhi

6 tháng 12 2016 - olm

Cho hai số tự nhiên a và b, trong đó a là số lẻ. Chứng minh rằng hai số a và a.b + 2\(^{2013}\) là hai số nguyên tố cùng nhau.

#Hỏi cộng đồng OLM #Toán lớp 6

Nguyễn Ngọc Anh Minh

6 tháng 12 2016

Gọi d là ƯSC(a; a.b + 2²⁰¹³)

=> a chia hết cho d và a.b + 2²⁰¹³ cũng chia hết cho d

Do a là số lẻ => d lẻ, 2²⁰¹³ là số chẵn mà d lẻ => 2²⁰¹³ chia hết cho d khi d = 1

=> a và a.b + 2²⁰¹³ là hai số nguyên tố cùng nhau

Đúng(0)

Khánh Linh

6 tháng 12 2016

Câu 6: Cho hai số tự nhiên a và b, trong đó a là số lẻ. Chứng minh rằng hai số a và a.b + 2\(^{2013}\) là hai số nguyên tố cùng nhau.

#Hỏi cộng đồng OLM #Toán lớp 6

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP