PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
26 tháng 8 2016
a) và b) mik ko bt làm.
c) Ta có a & b là số chẵn nên a*b = \(\frac{1}{2}a\cdot2.\frac{1}{2}b\cdot2\)= 4(\(\frac{1}{2}a\cdot b\)) suy ra đpcm
d) giống c ( \(2\cdot\frac{1}{2}a\cdot b\))
NT
1
7 tháng 2 2017
Gọi hai số đó là 2k+1;2k+3(k thuộc N) va UCLN(2k+1;2k+3)=d
=> \(\hept{\begin{cases}2k+1⋮d\\2k+3⋮d\end{cases}}\)
=>\(2k+1-2k+3⋮d\)
=>2 chia hết cho d =>UCLN(2k+1;2k+3) thuoc {1,2}
Mà 2k+1 và 2k+3 là số lẻ
=>UCLN(2k+1;2k+3)=1
=>2 số lẻ liên tiếp là 2 số nguyên tố cùng nhau
YC
1
15 tháng 10 2015
Gọi 2 số lẻ là 2k+1 và 2h+1
Tích chúng là:
\(\left(2k+1\right)\left(2h+1\right)=4kh+2k+2h+1=2.\left(2kh+k+h\right)+1\) là 1 số lẻ => đpcm
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
6 tháng 12 2016
Gọi d là ƯSC(a; a.b + 22013)
=> a chia hết cho d và a.b + 22013 cũng chia hết cho d
Do a là số lẻ => d lẻ, 22013 là số chẵn mà d lẻ => 22013 chia hết cho d khi d = 1
=> a và a.b + 22013 là hai số nguyên tố cùng nhau
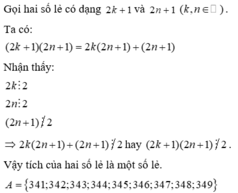
Sơ đồ con đường
Lời giải chi tiết
Gọi hai số lẻ có dạng 2k+1 và 2n+1 ( k , n ∈ ℕ ) .
Phân tích tích của 2 số vừa gọi và xét tính chia hết cho 2.
Để chứng minh tích đó là số lẻ thì tích đó không chia hết cho 2.
Gọi hai số lẻ có dạng 2k+1 và 2n+1 ( k , n ∈ ℕ ) .Ta có:
( 2 k + 1 ) ( 2 n + 1 ) = 2 k ( 2 n + 1 ) + ( 2 n + 1 )
Nhận thấy:
2 k ⋮ 2 2 n ⋮ 2 ( 2 n + 1 ) ⋮ 2 . ⇒ 2 k ( 2 n + 1 ) + ( 2 n + 1 ) ⋮ 2 h a y ( 2 k + 1 ) ( 2 n + 1 ) ⋮ 2
Vậy tích của hai số lẻ là một số lẻ.
A = 341 ; 342 ; 343 ; 344 ; 345 ; 346 ; 347 ; 348 ; 349