

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Vẽ tia AG là tia đối của tia AC
Ta có: \(\widehat{FAB}=\widehat{ABC}\)(hai góc so le trong, AF//BC)
\(\widehat{GAF}=\widehat{ACB}\)(hai góc đồng vị, AF//BC)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{BAF}=\widehat{GAF}\)
hay Ax là tia phân giác của góc ngoài tại đỉnh A(đpcm)

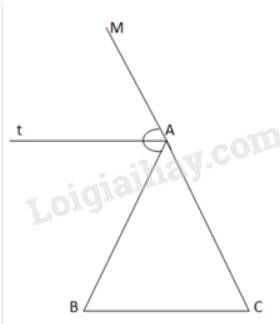
Gọi AM là tia đối của AC. At là đường phân giác của \(\widehat {MAB} \Rightarrow \widehat {MAt} = \widehat {BAt}\)
Ta có: \(At\parallel BC\) nên:
\(\widehat {ABC} = \widehat {BAt}\)(Hai góc sole trong)
\(\widehat {ACB} = \widehat {MAt}\)(Hai góc đồng vị)
Mà \(\widehat {MAt} = \widehat {BAt}\)\( \Rightarrow \widehat {ABC} = \widehat {ACB}\)
Vậy tam giác ABC cân tại A ( Dấu hiệu nhận biết tam giác cân).

VÌ \(Am//BC\)
\(\Rightarrow\widehat{mAC}=\widehat{ACB}\left(SLT\right)\left(1\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{ABC}\)ĐỒNG VỊ
MÀ\(\Rightarrow\widehat{A_1}=\widehat{mAC}\)( Am là tia phân giác của góc ngoài tại đỉnh A)
\(\Rightarrow\widehat{ABC}=\widehat{mAC}\left(2\right)\)
TỪ 1 VÀ 2
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
nên \(\Delta ABC\)là tam giác cân tại A
\(\Rightarrow AB=AC\left(đpcm\right)\)

b: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác