Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

À, mình nhầm. hình thang cân ABCD ( AB song song CD ) có 2 đường chéo cắt nhau tại P, 2 cạnh bên kéo dài cắt nhau tại Q. Chứng minh rằng : PQ là đường trung trực của 2 đáy

Bài 2 :
a) (2x + 1)(1 - 2x) + (2x - 1)2 = 22
=> 1 - 4x2 + (4x2 - 4x + 1) = 22
=> 1 - 4x2 + 4x2 + 4x + 1 = 22
=> 4x + 2 = 22
=> 4x = 20
=> x = 5
Vậy x = 5

Câu |
Khẳng định |
Đúng |
Sai |
1 |
Hình thang là tứ giác có các cạnh đối song song |
x |
|
2 |
Hình thang có hai cạnh bên bằng nhau là hình thang cân |
|
x |
3 |
Hình bình hành là tứ giác có hai đường chéo bằng nhau |
|
x |
4 |
Hình thang có hai cạnh bên song song là hình bình hành |
x |
|

"Hai đường chéo cắt nhau tại O và song song với đáy AB....". Câu này không đúng lắm. Bạn xem lại đề.

a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bằng nhau nên là hình bình hành theo dấu hiệu nhận biết 5
b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)
c) Sai.
Ví dụ tứ giác ABCD ở dưới có AB = CD nhưng không phải hình bình hành.
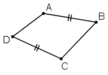
d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.
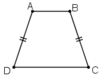
A B C D
Vẽ đường chéo AC.
Hình thang ABCD có: AB//CD
=> \(\widehat{BAC}=\widehat{ACD}\)
Xét \(\Delta ABC\)và \(\Delta ACD\)có:
- \(AB=CD\)
- \(\widehat{BAC}=\widehat{ACD}\)
- \(AC\) là cạnh chung
Do đó: \(\Delta ABC=\Delta ACD\left(c-g-c\right)\)
\(=>\widehat{DAC}=\widehat{BCA}\)(2 góc tương ứng nằm ở vị trí so le trong)
\(=>AD//BC\)
Hình vẽ:
A B C D
Vẽ đường chéo AC
Hình thang ABCD có: AB//CD
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\)
Xét \(\Delta ABC\)và \(\Delta ACD\)có:
\(-AB=CD\)
\(-\widehat{BAC}=\widehat{ACD}\)
\(-AC\)là cạnh chung
Do đó: \(\Delta ABC=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow\widehat{DAC}=\widehat{BCA}\)(2 góc tương ứng nằm ở vị trí so le trong)
\(\Rightarrow AD//BC\)