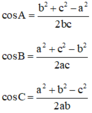NT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TM
11
Y
8 tháng 12 2021
1.Định lý pitago là một định lý quan trọng nhất trong tam giác vuông. Các bạn được học định lý này trong từ lớp 7 và nó dùng để để giải được các bài tập về tam giác, các bạn phải nắm vững chắc chắn kiến thức này.
2.Một số toán liên hệ căn bản trong hình học và giữa ba cạnh của một tam giác vuông.
8 tháng 12 2021
Ko k những người cop mạng hay trả lời sai chưa chi tiết
PT
30 tháng 3 2017
Định lí:
Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.
Ta có các hệ thức sau: a2 = b2 + c2 - 2bc.cosA (1)
b2 = a2 + c2 - 2bc.cosB (2)
c2 = a2 + b2 - 2bc.cosC (3)
Hệ quả: Từ định lí cosin suy ra:
cosA = cosB =
cosC =
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) Mệnh đề \(P \Rightarrow Q\), phát biểu là: “Nếu a và b chia hết cho c thì a + b chia hết cho c.”
Mệnh đề này đúng nên nó là một định lý.
Giả thiết của định lí: a và b chia hết cho c
Kết luận của định lí: a + b chia hết cho c
Phát biểu định lí dưới dạng điều kiện cần là: “ a + b chia hết cho c là điều kiện cần để có a và b chia hết cho c”
Phát biểu định lí dưới dạng điều kiện đủ là: “ a và b chia hết cho c là điều kiện đủ để có a + b chia hết cho c”
b) Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là mệnh đề \(Q \Rightarrow P\).
Mệnh đề \(Q \Rightarrow P\): “Nếu a + b chia hết cho c thì a và b chia hết cho c”
Mệnh đề này sai.
Chẳng hạn a = 1 và b = 2, c =3. Ta có: \(1 + 2 = 3\; \vdots \;3\), nhưng 1 và 2 không chia hết cho 3.
KK
30 tháng 3 2017
Do b là cạnh của tam giác nên b > 0
Đặt \(f\left(x\right)=b^2x^2-\left(b^2+c^2-a^2\right)x+c^2>0,\forall x\)
Theo định lý của dấu về tam thức bậc 2
\(\Rightarrow\left\{{}\begin{matrix}b^2>0\left(đúng\right)\\\Delta< 0\end{matrix}\right.\)\(\Rightarrow\Delta< 0\)
\(\Leftrightarrow\Delta=\left(b^2+c^2-a^2\right)^2-4b^2c^2< 0\)
Chứng minh rằng \(\Delta=\left(b^2+c^2-a^2\right)^2-4b^2c^2< 0\)
\(\Leftrightarrow\left(b^2+c^2-a^2\right)^2< 4b^2c^2\)
\(\Leftrightarrow b^2+c^2-a^2< 2bc\)
\(\Leftrightarrow b^2-2bc+c^2< a^2\)
\(\Leftrightarrow\left(b-c\right)^2< a^2\)
\(\Leftrightarrow b-c< a\)
\(\Leftrightarrow b< c+a\)
Theo bất đẳng thức tam giác thì \(b< c+a\)
\(\Rightarrow\)\(\Delta=\left(b^2+c^2-a^2\right)^2-4b^2c^2< 0\) ( đpcm )
Vậy \(f\left(x\right)=b^2x^2-\left(b^2+c^2-a^2\right)x+c^2>0,\forall x\)
CM
10 tháng 5 2019
Định lí Cô sin : Tam giác ABC có AB = c, BC = a, AC = c thì ta có :
